题目内容
19.设二次函数f(x)=ax2+bx+c(a,b,c为常数).若不等式f(x)≥2ax+b的解集为R,则$\frac{b^2}{{{a^2}+{c^2}}}$的最大值为2$\sqrt{2}$-2.分析 根据不等式恒大于等于0,求出c≥a,令c=ka(k>1),再根据基本不等式的性质求出代数式的最大值即可.
解答 解:ax2+(b-2a)x+c-b≥0(a>0),
△=(b-2a)2-4a(c-b)≤0,
即b2+4a2-4ac≤0,b2≤4ac-4a2,
∴$\frac{b^2}{{{a^2}+{c^2}}}≤\frac{{4ac-4{a^2}}}{{{a^2}+{c^2}}}$4ac-4a2≤b2,
∴c≥a,
求最大值、不妨令c=ka(k>1)
∴$\frac{{4ac-4{a^2}}}{{{a^2}+{c^2}}}=\frac{{4k{a^2}-4{a^2}}}{{{k^2}{a^2}+{a^2}}}=4\frac{k-1}{{{k^2}+1}}(k>1)$
令k-1=t,$\frac{{4ac-4{a^2}}}{{{a^2}+{c^2}}}=4\frac{t}{{{{(t+1)}^2}+1}}=4\frac{1}{{t+\frac{2}{t}+2}}≤\frac{4}{{2\sqrt{2}+2}}=2\sqrt{2}-2$
即$\frac{b^2}{{{a^2}+{c^2}}}≤2\sqrt{2}-2$,
故答案为:2$\sqrt{2}$-2.
点评 本题考查了二次函数的性质,考查基本不等式的性质以及转化思想,是一道中档题.

练习册系列答案
相关题目
9.已知函数f(x)=xlnx-aex(e为自然对数的底数)有两个极值点,则实数a的取值范围是( )
| A. | $({0,\frac{1}{e}})$ | B. | (0,e) | C. | $({\frac{1}{e},e})$ | D. | (-∞,e) |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{5}$=1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
| A. | $\sqrt{5}$ | B. | 3 | C. | 5 | D. | 4$\sqrt{2}$ |
16.已知正项数列{an}中,a1=1,a2=$\sqrt{3},2{a_n}^2={a_{n+1}}^2+{a_{n-1}}$2(n≥2),则a5=( )
| A. | 9 | B. | 6 | C. | $2\sqrt{3}$ | D. | 3 |
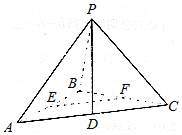 如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.
如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.