题目内容
20.在三角形ABC中,AD⊥BC,AD=1,BC=4,点E为AC的中点,$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$,则AB的长度为$\sqrt{2}$.分析 根据题意,画出图形,结合图形建立平面直角坐标系,利用坐标表示$\overrightarrow{DC}$•$\overrightarrow{BE}$,从而求出AB的长度.
解答 解:以D为原点,以BC,AD所在直线为x,y轴,
建立平面直角坐标系,如图所示;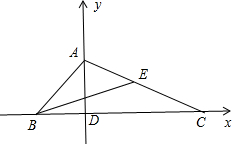
设BD=x,则CD=4-x,
D(0,0),A(0,1),B(-x,0),
C(4-x,0),E(2-$\frac{x}{2}$,$\frac{1}{2}$);
∴$\overrightarrow{DC}$=(4-x,0),$\overrightarrow{BE}$=(2+$\frac{x}{2}$,$\frac{1}{2}$),
∴$\overrightarrow{DC}$•$\overrightarrow{BE}$=(4-x)(2+$\frac{x}{2}$)+0×$\frac{1}{2}$=$\frac{15}{2}$,
化简得x2=1,
∵x>0,解得x=1,
∴B(-1,0);
又A(0,1),
∴|AB|=$\sqrt{{1}^{2}{+(-1)}^{2}}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了平面向量的数量积应用问题,解题时建立平面直角坐标系,利用向量的坐标解决向量问题,是基础题.

练习册系列答案
相关题目
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{5}$=1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
| A. | $\sqrt{5}$ | B. | 3 | C. | 5 | D. | 4$\sqrt{2}$ |
16.已知正项数列{an}中,a1=1,a2=$\sqrt{3},2{a_n}^2={a_{n+1}}^2+{a_{n-1}}$2(n≥2),则a5=( )
| A. | 9 | B. | 6 | C. | $2\sqrt{3}$ | D. | 3 |
17.函数f(x)=x3-3x2+1是减函数的单调区间为( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (-∞,0) | D. | (0,2) |
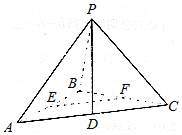 如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.
如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.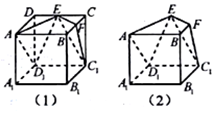 如图,在图(1)的正方体ABCD-A1B1C1D1中,E、F分别为CD、BC的中点,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为( )
如图,在图(1)的正方体ABCD-A1B1C1D1中,E、F分别为CD、BC的中点,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为( )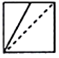



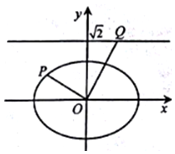 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1.