题目内容

16．若集合A={x|x2＜4}，B={y|y=x2-2x-1，x∈A}，则集合A∪B={x|-2≤x＜7}．

分析 解不等式求得集合A，求函数的值域得集合B，根据并集的定义求出A∪B．

解答 解：集合A={x|x2＜4}={x|-2＜x＜2}，
B={y|y=x2-2x-1，x∈A}={y|y=（x-1）2-2，x∈A}
={y|-2≤x＜7}，
则集合A∪B={x|-2≤x＜7}．
故答案为：{x|-2≤x＜7}．

点评 本题考查了解不等式与求函数的值域问题，也考查了集合的运算问题，是基础题．

练习册系列答案
相关题目
6．已知定义[x]表示不超过的最大整数，如[2]=2，[2，2]=2，执行如图所示的程序框图，则输出S=（　　）
A．1991B．2000C．2007D．2008
7．已知函数$f（x）=\frac{1-x}{ax}+lnx$在（1，+∞）上是增函数，且a＞0．
（Ⅰ）求a的取值范围；
（Ⅱ）求函数g（x）=ln（1+x）-x在[0，+∞）上的最大值；
（Ⅲ）已知a＞1，b＞0，证明：$\frac{1}{a+b}≤ln\frac{a+b}{b}＜\frac{a}{b}$．
4．已知数列{an}中，a1=1，a2=3，其前n项和Sn满足Sn+1+Sn-1=2Sn+1，其中n≥2，n∈N*．
（1）求证：数列{an}为等差数列，并求其通项公式；
（2）设bn=$\frac{a_n}{2^n}\;，\;\;{T_n}$为数列{bn}的前n项和，求Tn；
（3）设cn=4n+（-1）n-1λ•2an（λ为非零整数，n∈N*），试确定实数λ的值，使得对任意的n∈N*，都有cn+1＞cn成立．
11．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{5}$=1的右焦点与抛物线y2=12x的焦点重合，则该双曲线的焦点到其渐近线的距离等于（　　）
A．$\sqrt{5}$B．3C．5D．4$\sqrt{2}$
1．在△ABC中，角A，B，C所对的边为a，b，c．已知c2=a2+b2-4bccosC，且A-C=$\frac{π}{2}$．
（Ⅰ）求cosC的值；
（Ⅱ）求cos（B+$\frac{π}{3}$）的值．
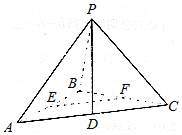8．如图，在三棱锥P-ABC中，PB⊥面ABC，△ABC是直角三角形，∠ABC=90°，AB=BC=2，∠PAB=45°，点D、E、F分别为AC、AB、BC的中点．
（1）求证：EF⊥PD；
（2）求直线PF与平面PBD所成的角的正弦值．
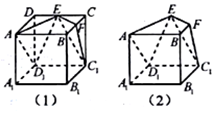5．如图，在图（1）的正方体ABCD-A1B1C1D1中，E、F分别为CD、BC的中点，将图（1）中的正方体截去两个三棱锥，得到图（2）中的几何体，则该几何体的侧视图为（　　）
A．B．C．D．
13．有以下几种说法：（l1、l2不重合）
①若直线l1，l2都有斜率且斜率相等，则l1∥l2； 
 ②若直线l1⊥l2，则它们的斜率互为负倒数；   
③两条直线的倾斜角相等，则这两条直线平行；  
④只有斜率相等的两条直线才一定平行．   
以上说法中正确的个数是（　　）
A．1B．2C．3D．0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网