题目内容
18.已知实数x,y满足条件$\left\{\begin{array}{l}3x+y+3≥0\\ 2x-y+2≤0\\ x+2y-4≤0\end{array}\right.$,则z=x2+y2的取值范围为( )| A. | [1,13] | B. | [1,4] | C. | $[{\frac{4}{5},13}]$ | D. | $[{\frac{4}{5},4}]$ |
分析 根据已知的约束条件画出满足约束条件的可行域,再用图象判断,求出目标函数的最大值.
解答 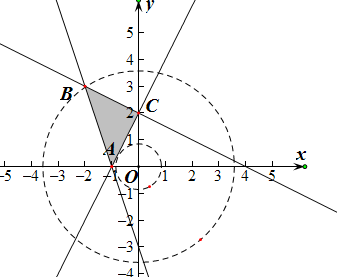 解:$\left\{\begin{array}{l}3x+y+3≥0\\ 2x-y+2≤0\\ x+2y-4≤0\end{array}\right.$的可行域如图所示,其中A(-1,0),B(-2,3),C(0,2),
解:$\left\{\begin{array}{l}3x+y+3≥0\\ 2x-y+2≤0\\ x+2y-4≤0\end{array}\right.$的可行域如图所示,其中A(-1,0),B(-2,3),C(0,2),
若目标函数z=x2+y2的几何意义是可行域内的点到坐标原点距离的平方.由图形可知仅在点B(-2,3)取得最大值,z=4+9=13.
由图知,原点到直线2x-y+2=0的距离最小,d=$\frac{2}{\sqrt{5}}$,
可得z=x2+y2=d2=$\frac{4}{5}$.
则z=x2+y2的取值范围为[$\frac{4}{5}$,13],
故选:C.
点评 用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.判断几何意义,最后比较,即可得到目标函数的最优解.

练习册系列答案
相关题目
9.已知函数f(x)=xlnx-aex(e为自然对数的底数)有两个极值点,则实数a的取值范围是( )
| A. | $({0,\frac{1}{e}})$ | B. | (0,e) | C. | $({\frac{1}{e},e})$ | D. | (-∞,e) |
6.已知定义[x]表示不超过的最大整数,如[2]=2,[2,2]=2,执行如图所示的程序框图,则输出S=( )

| A. | 1991 | B. | 2000 | C. | 2007 | D. | 2008 |
3.设集合A={x|0≤x≤2},B={x∈N|1≤x≤3},则A∩B=( )
| A. | {1,2} | B. | {1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |
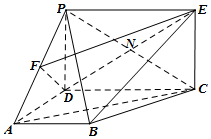 如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1. 四边形PDCE为矩形,线段PC交DE于点N.
如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1. 四边形PDCE为矩形,线段PC交DE于点N.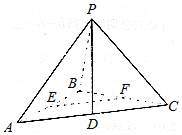 如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.
如图,在三棱锥P-ABC中,PB⊥面ABC,△ABC是直角三角形,∠ABC=90°,AB=BC=2,∠PAB=45°,点D、E、F分别为AC、AB、BC的中点.