题目内容
19.对于给定的正整数n,若等差数列a1,a2,a3,…满足a12+a2n+12≤10,则S=a2n+1+a2n+2+a2n+3+…+a4n+1的最大值为10n+5.分析 根据等差数列的关系整理得S=(2n+1)a3n+1,由a12+a2n+12≤10得到关于d的二次方程,10n2d2-8da3n+1+2a3n+12-10≤0有解,根据判别式即可求出.
解答 解:因为数列a2n+1+a4n+1=a2n+2+a4n=…=2a3n+1是等差数列,
所以a12+a2n+12=(a3n+1-3nd)2+(a3n+1-nd)2≤10,
化简得:2a3n+12-8da3n+1+10n2d2-10≤0,
关于d的二次方程,10n2d2-8da3n+1+2a3n+12-10≤0,有解,
所以△=64a3n+12-4×10n2(2a3n+12-10)≥0,
所以(64-80n2)a3n+12≥-400n2,
所以a3n+12≤$\frac{400{n}^{2}}{80{n}^{2}-64}$=10($\frac{1}{2}$+$\frac{2}{5{n}^{2}-4}$)≤25,
所以-5≤a3n+1≤5,
即Sn≤5(2n+1)=10n+5,
故答案为:10n+5.
点评 本题考查求等差数列的和,利用判别式判断二次函数的最大值,属于中档题.

练习册系列答案
相关题目
10.函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象如图所示,则( )
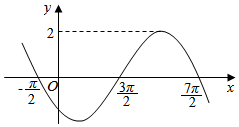

| A. | A=2,ω=2,φ=$\frac{3π}{4}$ | B. | A=2,ω=2,φ=$\frac{5π}{4}$ | C. | A=2,ω=$\frac{1}{2}$,φ=$\frac{3π}{4}$ | D. | A=2,ω=$\frac{1}{2}$,φ=$\frac{5π}{4}$ |
7.已知x,y满足约束条件$\left\{\begin{array}{l}x-y+5≥0\\ x≤2\\ x+y≥0\end{array}\right.$,则z=x+2y的最小值为( )
| A. | -3 | B. | $-\frac{5}{2}$ | C. | -2 | D. | $\frac{5}{2}$ |
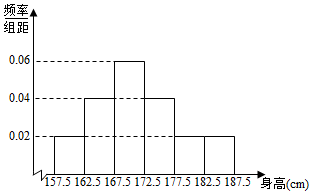 某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.
某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.