题目内容

15．设函数f（x）=3x+9x，则f（log32）=6．

分析 利用对数换底公式直接求解．

解答 解：∵函数f（x）=3x+9x，
∴f（log32）=${3}^{lo{g}_{3}2}+{9}^{lo{g}_{3}2}$=2+${9}^{lo{g}_{9}4}$=2+4=6．
故答案为：6．

点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意对数换底公式的合理运用．

练习册系列答案
相关题目
15．双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的两条渐近线互相垂直，F1，F2分别为C的左，右焦点，P点在该双曲线的右支上且到直线x=-$\frac{{\sqrt{2}}}{2}$a的距离为3$\sqrt{2}$，若|PF1|+|PF2|=8，则双曲线的标准方程为（　　）
A．$\frac{x^2}{4}-\frac{y^2}{4}=1$B．$\frac{x^2}{8}-\frac{y^2}{8}=1$C．$\frac{x^2}{16}-\frac{y^2}{16}=1$D．以上答案都不对
16．已知抛物线C：y2=8x的焦点为F，准线l与x轴的交点为M，过点M的直线l′与抛物线C的交点为P，Q，延长PF交抛物线C于点A，延长QF交抛物线C于点B，若$\frac{|PF|}{|AF|}$+$\frac{|QF|}{|BF|}$=22，则直线l′的方程为y=±$\frac{\sqrt{6}}{6}$（x+2）．
3．设集合A={x|f（x）=x}，B={x|f[f（x）]=x}，设f（x）=x2-（2a-1）x+a2（常数a∈R），求证：A=B．
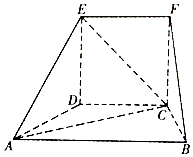10．在如图所示的几何体中，四边形CDEF为正方形，四边形ABCD为等腰梯形，AB∥CD，AB=2BC，∠BAC=30°，AC⊥FB．
（Ⅰ）求证：AC⊥平面FBC；
（Ⅱ）求FC与平面EAC所成角的正弦值．
20．设函数f（x）=$\frac{{x}^{3}}{3}$-$\frac{3a+2}{2}$x2+6ax+b，其中a，b∈R．
（1）若函数f（x）在x=1处取得极值-$\frac{1}{6}$，求a，b的值；
（2）求函数f（x）的单调递增区间．
7．已知等差数列{an}的首项为a1（a1≠0），公差为d，且不等式a1x2-3x+2＜0的解集为（1，d）
（1）求数列{an}的通项公式；
（2）若数列{bn}满足bn-an=$\frac{1}{{n}^{2}+n}$，求数列{bn}的前n项和Sn．
4．在直角坐标系xOy中，动圆M与圆${O_1}：{x^2}+2x+{y^2}=0$外切，同时与圆${O_2}：{x^2}+{y^2}-2x-24=0$内切．
（1）求动圆圆心M的轨迹方程；
（2）设动圆圆心M的轨迹为曲线C，设A，P是曲线C上两点，点A关于x轴的对称点为B（异于点P），若直线AP，BP分别交x轴于点S，T，证明：|OS|•|OT|为定值．
5．已知R为实数集，集合A={x|x2-2x-3≥0}，则∁RA=（　　）
A．（-1，3）B．[-1，3]C．（-3，1）D．[-3，1]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网