题目内容
4.在直角坐标系xOy中,动圆M与圆${O_1}:{x^2}+2x+{y^2}=0$外切,同时与圆${O_2}:{x^2}+{y^2}-2x-24=0$内切.(1)求动圆圆心M的轨迹方程;
(2)设动圆圆心M的轨迹为曲线C,设A,P是曲线C上两点,点A关于x轴的对称点为B(异于点P),若直线AP,BP分别交x轴于点S,T,证明:|OS|•|OT|为定值.
分析 (1)求出两个圆的圆心与半径,设动圆圆心M(x,y),推出|MO1|+|MO2|=6>|O1O2|,由椭圆定义知,圆心M的轨迹为椭圆,求解动圆圆心M的轨迹方程即可.
(2)设P(x0,y0),A(x1,y1),S(xS,0),T(xT,0),则B(x1,-y1),求出:|OS|•|OT|的表达式,通过P(x0,y0)和A(x1,y1)在椭圆$\frac{x^2}{9}+\frac{y^2}{8}=1$上,化简求解即可.
解答 解:(1)由圆${O_1}:{x^2}+2x+{y^2}=0$,得(x+1)2+y2=1,所以O1(-1,0),半径为1;由圆${O_2}:{x^2}+{y^2}-2x-24=0$,得(x-1)2+y2=25,所以O2(1,0),半径为5,设动圆圆心M(x,y),半径为R,因为⊙M与⊙O1外切,所以|MO1|=R+1,又因为⊙M与⊙O2外切,所以|MO2|=5-R,将两式相加得|MO1|+|MO2|=6>|O1O2|,由椭圆定义知,圆心M的轨迹为椭圆,且2a=6,c=1,则a2=9,b2=8,所以动圆圆心M的轨迹方程为$\frac{x^2}{9}+\frac{y^2}{8}=1$.
(2)证明:设P(x0,y0),A(x1,y1),S(xS,0),T(xT,0),则B(x1,-y1),由题意知x0≠±x1.则${k_{AP}}=\frac{{{y_1}-{y_0}}}{{{x_1}-{x_0}}}$,直线AP方程为y-y1=kAP(x-x1),令y=0,得${x_S}=\frac{{{x_0}{y_1}-{x_1}{y_0}}}{{{y_1}-{y_0}}}$,同理${x_T}=\frac{{{x_0}({-{y_1}})-{x_1}{y_0}}}{{({-{y_1}})-{y_0}}}=\frac{{{x_0}{y_1}+{x_1}{y_0}}}{{{y_1}+{y_0}}}$,于是$|{OS}|•|{OT}|=|{{x_S}{x_T}}|=|{\frac{{{x_0}{y_1}-{x_1}{y_0}}}{{{y_1}-{y_0}}}•\frac{{{x_0}{y_1}+{x_1}{y_0}}}{{{y_1}+{y_0}}}}|=|{\frac{{{x_0}^2{y_1}^2-{x_1}^2{y_0}^2}}{{{y_1}^2-{y_0}^2}}}|$,
又P(x0,y0)和A(x1,y1)在椭圆$\frac{x^2}{9}+\frac{y^2}{8}=1$上,故${y_0}^2=8({1-\frac{{{x_0}^2}}{9}}),{y_1}^2=8({1-\frac{{{x_1}^2}}{9}})$,则${y_1}^2-{y_0}^2=\frac{8}{9}({{x_0}^2-{x_1}^2}),{x_0}^2{y_1}^2-{x_1}^2{y_0}^2=8{x_0}^2({1-\frac{{{x_1}^2}}{9}})-8{x_1}^2({1-\frac{{{x_0}^2}}{9}})=8({{x_0}^2-{x_1}^2})$.
所以$|{OS}|•|{OT}|=|{\frac{{{x_0}^2{y_1}^2-{x_1}^2{y_0}^2}}{{{y_1}^2-{y_0}^2}}}|=|{\frac{{8({{x_0}^2-{x_1}^2})}}{{\frac{8}{9}({{x_0}^2-{x_1}^2})}}}|=9$.
点评 本题考查轨迹方程的求法,椭圆的简单性质的应用,圆锥曲线有关的定值问题的求法,考查转化思想,设而不求方法的应用,考查分析问题解决问题的能力.

| 套餐名称 | 月套餐费(单位;元) | 月套餐流量(单位,M) |
| A | 20 | 300 |
| B | 30 | 500 |
小王过去50个月的手机月使用流量(单位:M)频率分布表如下:
| 月使用流量分组 | [100,200] | (200,300] | (300,400] | (400,500] | (500,600] | (600,700] |
| 频数 | 4 | 11 | 12 | 18 | 4 | 1 |
(1)若小王订购A套餐,假设其手机月实际使用流量为x(单位:M,100≤x≤700)月流量费用y(单位:元),将y表示为x的函数;
(2)小王拟从A套餐或B套餐中选订一款,若以月平均费用作为决策依据,他应订购哪一种套餐?并说明理由.
| A. | 24 | B. | 28 | C. | 32 | D. | 16 |
| A. | (-ln2,0)∪(3,+∞) | B. | (-ln2,+∞) | C. | (3,+∞) | D. | (-ln2,0) |
| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
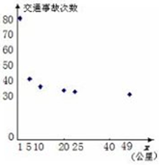
(Ⅰ)把界桩公里数1001记为x=1,公里数1005记为x=5,…,数据绘成的散点图如图所示,以x为解释变量、交通事故数y为预报变量,请在y=a+be-x和y=a+$\frac{b}{x}$间选取一个建立回归方程表述x,y二者之间的关系(a,b的值精确到0.1);
(Ⅱ)若保险公司在2015年交通事故中随机抽取100例,理赔60万元的有1例,理赔2万元的有19例,理赔0.2万元的有80例.
利用你得到的回归方程,试预报这一年在界桩1040公里附近处发生的交通事故的理赔费(理赔费精确到0.1万元).
附:回归直线v=$\widehat{α}$+$\widehat{β}$u的斜率和截距的最小二乘法估计分别为:
$\widehat{β}$=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$.
一些量的计算值:
| $\overline{x}$ | $\overline{y}$ $\overline{ω}$ $\overline{φ}$ | $\sum_{i=1}^{6}({ω}_{i}-\overline{ω})^{2}$ | $\sum_{i=1}^{6}({φ}_{i}-\overline{φ})^{2}$ | $\sum_{i=1}^{6}({ω}_{i}-\overline{ω})({y}_{i}-\overline{y})$ | $\sum_{i=1}^{6}({φ}_{i}-\overline{φ})({y}_{i}-\overline{y})$ |
| 18.3 | 41.7 0.235 0.062 | 0.723 | 0.112 | 36.3 | 14.1 |
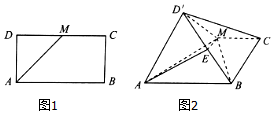 如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.