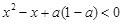题目内容
已知函数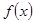 是
是 上的增函数,设
上的增函数,设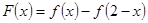 。
。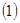 用定义证明:
用定义证明: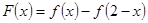 是
是 上的增函数;(6分)
上的增函数;(6分)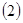 证明:如果
证明:如果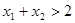 ,则
,则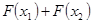 >0,(6分)
>0,(6分)
(1)证明见解析(2)证明见解析
解析试题分析:(1)任取 ,
,


=

 ,
, ,
, , 又
, 又 是增函数,
是增函数,
 ,
,
且 ,
,



 ,
,
即 ,故
,故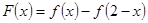 是增函数. ……6分
是增函数. ……6分
(2)由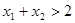 ,得
,得 且
且 又
又 是增函数,
是增函数, ,
, ,
,



 ,
,
即 . ……12分
. ……12分
考点:本小题主要考查抽象函数单调性的证明和应用,考查学生的逻辑推理能力和论证能力.
点评:解决抽象函数问题的主要方法是“赋值法”,证明抽象函数单调性也必须按照定义严格证明.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 .
. 在
在 上的最大值;
上的最大值; 时,
时, 对所有的
对所有的 及
及 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 对任意实数
对任意实数 都有
都有 ,
,
 的值;
的值;
 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论.
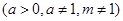 是奇函数.
是奇函数. 的值;
的值;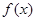 在
在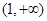 上的单调性,并给出证明;
上的单调性,并给出证明;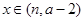 时,函数
时,函数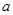 与
与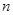 的值。
的值。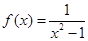 .
. 的定义域为A,求集合A;
的定义域为A,求集合A;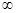 )上单调性,并用定义加以证明.
)上单调性,并用定义加以证明.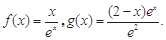
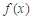 的极值;
的极值;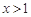 时,
时,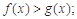
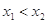 ,且
,且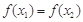 ,求证:
,求证: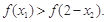
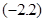 上的奇函数
上的奇函数 ,满足
,满足 ,又当
,又当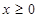 时,
时,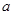 的取值范围。
的取值范围。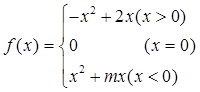
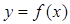 的图象;
的图象; 在区间[-1,
在区间[-1, -2]上单调递增,试确定
-2]上单调递增,试确定
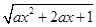 的定义域为R,解关于x的不等式
的定义域为R,解关于x的不等式