题目内容
(本题满分13分)已知函数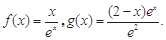
(1) 求函数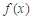 的极值;
的极值;
(2)求证:当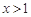 时,
时,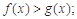
(3)如果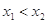 ,且
,且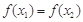 ,求证:
,求证: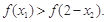
(1) 当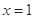 时,
时,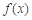 取得极大值
取得极大值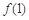 =
= ;
;
(2) 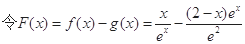 ,则只需证当
,则只需证当 时,
时,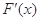 >0;
>0;
(3) 由⑵的结论知 时,
时,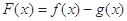 >0,∴
>0,∴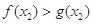 .
.
∵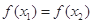 ,∴
,∴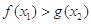 .
.
又 ,∴
,∴ 。
。
解析试题分析:⑴∵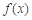 =
=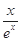 ,∴
,∴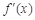 =
= . 2分
. 2分
令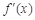 =0,解得
=0,解得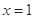 .
.
∴当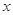
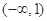
1 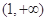
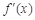
+ 0 - 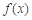
↗ 极大值 
↘ 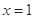 时,
时,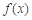 取得极大值
取得极大值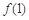 =
= . 4分
. 4分
⑵证明: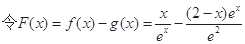 ,则
,则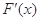 =
=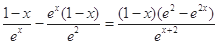 . 6分
. 6分
当 时,
时,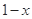 <0,
<0,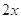 >2,从而
>2,从而 <0,
<0,
∴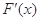 >0,
>0,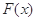 在
在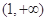 是增函数.
是增函数.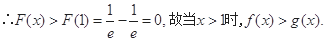 8分
8分
⑶证明:∵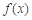 在
在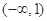 内是增函数,在
内是增函数,在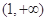 内是减函数.
内是减函数.
∴当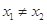 ,且
,且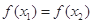 时,
时,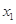 、
、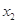 不可能在同一单调区间内.
不可能在同一单调区间内.
∴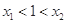 , 11分
, 11分
由⑵的结论知 时,
时,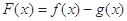 >0,∴
>0,∴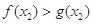 .
.
∵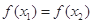 ,∴
,∴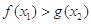 .
.
又 ,∴
,∴ 13分
13分
考点:利用导数研究函数的极值;利用导数研究函数的单调性。
点评:此题是个难题.主要考查函数与导数的综合应用能力,具体涉及到用导数来研

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
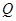 (百件)与销售价格
(百件)与销售价格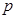 (元)的关系如下图,每月各种开支2000元.
(元)的关系如下图,每月各种开支2000元.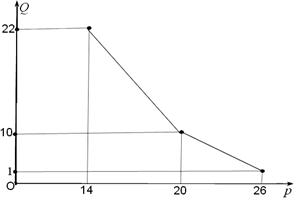
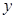 (元)与销售价格
(元)与销售价格 =
=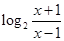 .
.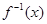 ,并求使得函数
,并求使得函数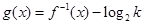 有零点的实数
有零点的实数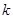 的取值范围.
的取值范围.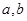 是方程
是方程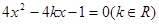 的两个不等实根,函数
的两个不等实根,函数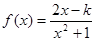 的定义域为
的定义域为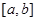 .
.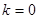 时,求函数
时,求函数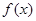 的值域;
的值域;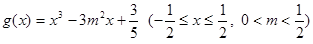 ,
, 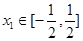 ,总存在
,总存在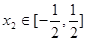 ,使得
,使得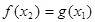 成立,
成立,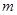 的取值范围.
的取值范围.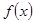 是
是 上的增函数,设
上的增函数,设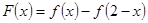 。
。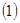 用定义证明:
用定义证明: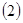 证明:如果
证明:如果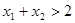 ,则
,则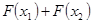 >0,(6分)
>0,(6分)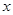 均有
均有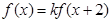 ,其中常数k为负数,且
,其中常数k为负数,且 在区间
在区间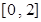 上有表达式
上有表达式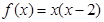
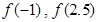 的值;
的值;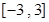 上的表达式,并讨论函数
上的表达式,并讨论函数 为奇函数,
为奇函数, 为常数.
为常数. 在区间
在区间 内单调递增;
内单调递增; 的值,不等式
的值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.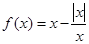 .
.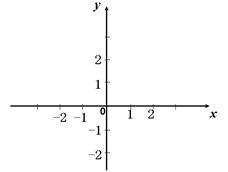
 的图象;
的图象; .
. 在
在 上是单调递增函数;
上是单调递增函数; 时,求函数在
时,求函数在 上的最值;
上的最值; 上恒有
上恒有 成立,求
成立,求 的取值范围.
的取值范围.