题目内容
(本题满分12分)已知函数y=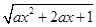 的定义域为R,解关于x的不等式
的定义域为R,解关于x的不等式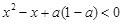
当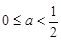 时,
时, ;当
;当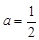 时,Ф;当
时,Ф;当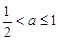 时,
时,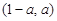 .
.
解析试题分析:由条件可得0≤a≤1,原不等式可化为(x-a)[x-(1-a)]>0,分0≤a< 、a=
、a= 、
、 <a≤1三种情况,分别求出不等式的解集.
<a≤1三种情况,分别求出不等式的解集.
解:∵函数y=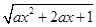 的定义域为R,∴
的定义域为R,∴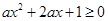 恒成立. …1分
恒成立. …1分
当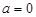 时,
时,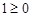 ,不等式恒成立;当
,不等式恒成立;当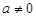 时,则
时,则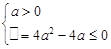
解得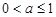 .综上,
.综上,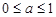 ………………………4分
………………………4分
由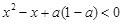 得
得 .……6分
.……6分
∵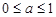 ,
,
∴(1)当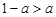 ,即
,即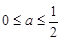 时,
时,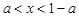 ;
;
(2)当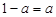 ,即
,即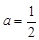 时,
时, ,不等式无解;
,不等式无解;
(3)当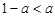 ,即
,即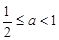 时,
时,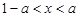 .………………………………10分
.………………………………10分
∴原不等式的解集为:当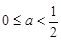 时,
时, ;当
;当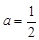 时,Ф;当
时,Ф;当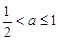 时,
时,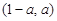 . ……………………12分
. ……………………12分
考点:本试题主要考查了二元一次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.
点评:解决该试题的关键是由条件可得0≤a≤1,对于参数a,分0≤a< 、a=
、a= 、
、 <a≤1三种情况,分别求出不等式的解集.
<a≤1三种情况,分别求出不等式的解集.

练习册系列答案
相关题目
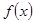 是
是 上的增函数,设
上的增函数,设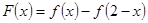 。
。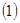 用定义证明:
用定义证明: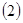 证明:如果
证明:如果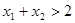 ,则
,则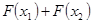 >0,(6分)
>0,(6分) 定义在R上的偶函数,当
定义在R上的偶函数,当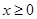 时,
时,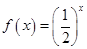
 ,
,  ,求:
,求: 的定义域。 (2)求使
的定义域。 (2)求使 的
的 的取值范围。
的取值范围。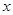 )=
)=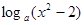 , 若
, 若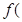 2)=1;
2)=1;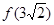 的值;
的值;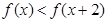
 .
. 在
在 上是单调递增函数;
上是单调递增函数; 时,求函数在
时,求函数在 上的最值;
上的最值; 上恒有
上恒有 成立,求
成立,求 的取值范围.
的取值范围. 的函数
的函数 同时满足:
同时满足: ,总有
,总有 ; ②
; ② ;
; ,则有
,则有 成立。
成立。 的值;
的值; ,总有
,总有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。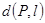 。
。 ,线段
,线段 ,求
,求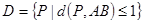 所表示图形的面积;
所表示图形的面积; 所表示的图形。(本题满分14分)
所表示的图形。(本题满分14分) 在
在 上的单调性.
上的单调性.