题目内容
(本题满分8分)已知奇函数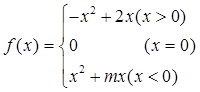
(1)求实数m的值,并在给出的直角坐标系中画出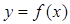 的图象;
的图象;
(2)若函数 在区间[-1,
在区间[-1, -2]上单调递增,试确定
-2]上单调递增,试确定 的取值范围.
的取值范围.
(1)2,图像见解析;(2) 。
。
解析试题分析:(1)当x<0时,-x>0,f(x)=-(x)2+2(-x)=-x2-2x,
又f(x)为奇函数,f(x)=-f(-x)=x2+2x,
所以m=2.……3分
f(x)的图象略.……5分
(2)由(1)知 =
= ,由图象可知,
,由图象可知, 在[-1,1]上单调递增,要使
在[-1,1]上单调递增,要使 在[-1,
在[-1, -2]上单调递增,只需
-2]上单调递增,只需 解之得
解之得  8分
8分
考点:本题考查分段函数;函数的奇偶性;函数的单调性;函数的图像;函数解析式的求法。
点评:本题求 的解析式是关键。利用函数的奇偶性求函数的解析式,一般情况下,求谁设谁,然后再根据
的解析式是关键。利用函数的奇偶性求函数的解析式,一般情况下,求谁设谁,然后再根据 与
与 的关系进行转换。
的关系进行转换。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
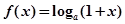 ,
,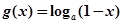 ,其中
,其中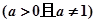 ,设
,设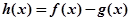 .
.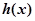 的奇偶性,并说明理由;
的奇偶性,并说明理由;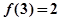 ,求使
,求使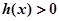 成立的x的集合。
成立的x的集合。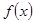 是
是 上的增函数,设
上的增函数,设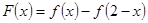 。
。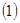 用定义证明:
用定义证明: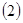 证明:如果
证明:如果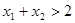 ,则
,则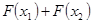 >0,(6分)
>0,(6分) 为奇函数,
为奇函数, 为常数.
为常数. 在区间
在区间 内单调递增;
内单调递增; 的值,不等式
的值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. (
( ,
,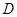 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数
 ,使函数
,使函数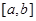 上的值域为
上的值域为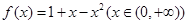 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;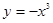 (
(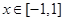 )为闭函数;
)为闭函数; 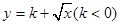 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围. 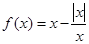 .
.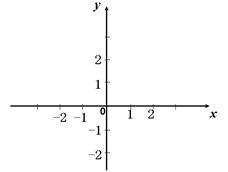
 的图象;
的图象; 定义在R上的偶函数,当
定义在R上的偶函数,当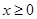 时,
时,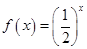
 ,
,  ,求:
,求: 的定义域。 (2)求使
的定义域。 (2)求使 的
的 的取值范围。
的取值范围。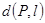 。
。 ,线段
,线段 ,求
,求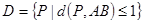 所表示图形的面积;
所表示图形的面积; 所表示的图形。(本题满分14分)
所表示的图形。(本题满分14分)