题目内容
(本小题满分14分)
设函数 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 在
在 上的最大值;
上的最大值;
(Ⅲ)当 时,
时, 对所有的
对所有的 及
及 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) 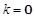 (2)
(2) 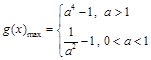 (3)
(3) 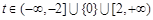
解析试题分析:(Ⅰ)由 得
得 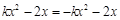 ,
,
∴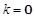 .································· 2分
.································· 2分
(Ⅱ)∵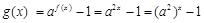 ·················· 3分
·················· 3分
①当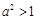 ,即
,即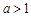 时,
时,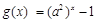 在
在 上为增函数,
上为增函数,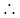
 最大值为
最大值为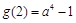 .······················· 5分
.······················· 5分
②当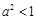 ,即
,即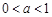 时,
时,
∴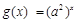 在
在 上为减函数,
上为减函数,
∴ 最大值为
最大值为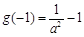 .······················· 7分
.······················· 7分
∴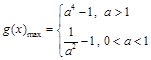 ························· 8分
························· 8分
(Ⅲ)由(Ⅱ)得 在
在 上的最大值为
上的最大值为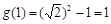 ,
,
∴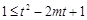 即
即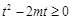 在
在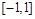 上恒成立················ 10分
上恒成立················ 10分
令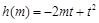 ,
,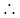
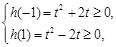
即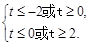
所以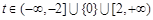 . 14分
. 14分
考点:本试题主要是考查了二次函数的性质以及不等式恒成立问题的运用。
点评:对于二次函数的性质主要是对称性的运用,同时遇到不等式的恒成立问题,一般要采用分离参数的思想来得到其取值范围。属于中档题,有一定的难度。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 ,设
,设 。
。 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出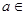 R,函数
R,函数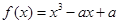 .
.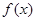 的单调区间;
的单调区间;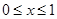 时,
时,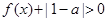 .
. (
( 且
且 ).
). 的定义域;
的定义域; 的
的 取值范围.
取值范围.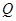 (百件)与销售价格
(百件)与销售价格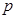 (元)的关系如下图,每月各种开支2000元.
(元)的关系如下图,每月各种开支2000元.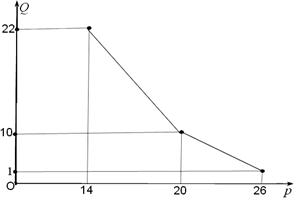
 (元)与销售价格
(元)与销售价格 ∈R,函数
∈R,函数 =
=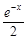 (
(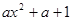 ),其中e是自然对数的底数.
),其中e是自然对数的底数.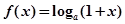 ,
,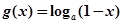 ,其中
,其中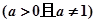 ,设
,设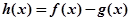 .
.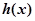 的奇偶性,并说明理由;
的奇偶性,并说明理由;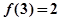 ,求使
,求使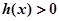 成立的x的集合。
成立的x的集合。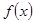 是
是 上的增函数,设
上的增函数,设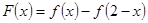 。
。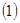 用定义证明:
用定义证明: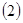 证明:如果
证明:如果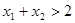 ,则
,则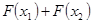 >0,(6分)
>0,(6分)