题目内容
4．已知数列{an}中，a1=1，an+1=2an+3，数列{bn}中，b1=1，且点（bn+1，bn）在直线y=x-1上．（Ⅰ） 求数列{an}的通项公式；
（Ⅱ）求数列{bn}的通项公式；
（Ⅲ）求数列{bn}的前n项和Sn．
分析 （Ⅰ）由an+1=2an+3得an+1+3=2（an+3），由此能求出an．
（Ⅱ）因为（bn+1，bn）在直线y=x-1上，所以bn=bn+1-1即bn+1-bn=1，由此能求出bn．
（Ⅲ）根据等差数列的前n项和公式进行解答．
解答 解：（Ⅰ）由an+1=2an+3得an+1+3=2（an+3）
所以{an+3}是首项为a1+3=4，公比为2的等比数列．
所以an+3=4×2n-1=2n+1，故an=2n+1-3；
（Ⅱ）因为（bn+1，bn）在直线y=x-1上，
所以bn=bn+1-1即bn+1-bn=1又b1=1
故数列{bn}是首项为1，公差为1的等差数列，
所以bn=n；
（Ⅲ）由（Ⅱ）知，数列{bn}是首项为1，公差为1的等差数列，
所以Sn=1×n+$\frac{1}{2}$n（n-1）=$\frac{1}{2}$n（n+1）．
点评 本题考查数列的通项公式的计算和等差数列的前n项和公式的应用，难度不大，考查计算能力．解题时要认真审题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
12．命题“?x0∈∁RQ，x03∈Q”的否定是（ ）
| A． | ?x0∉∁RQ，x03∈Q | B． | ?x0∈∁RQ，x03∈Q | C． | ?x∉∁RQ，x3∈Q | D． | ?x∈∁RQ，x3∉Q |
19．已知数列{an}满足a1=1，a2=$\frac{2}{3}$ 且 $\frac{1}{{a}_{n+1}}$+$\frac{1}{{a}_{n-1}}$=$\frac{2}{{a}_{n}}$（n≥2），则a15等于（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{7}$ | C． | $\frac{1}{3}$ | D． | $\frac{8}{15}$ |
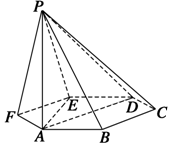如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，则下列结论正确的序号是④．