题目内容
17.若抛物线y2=8x上有一点P,它到焦点的距离为20,则P点的横坐标为18.分析 由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,已知|MF|=20,则M到准线的距离也为20,即可得|MF|=x+$\frac{p}{2}$=x+2=20,进而求出x.
解答 解:∵抛物线y2=8x=2px,
∴p=4,
由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,
∴|MF|=x+$\frac{p}{2}$=x+2=20,
∴x=18,
故答案为:18.
点评 活用抛物线的定义是解决抛物线问题最基本的方法.抛物线上的点到焦点的距离,叫焦半径.到焦点的距离常转化为到准线的距离求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知曲线y=Asinωx+a(A>0,ω>0)在区间$[0,\frac{2π}{ω}]$上截直线y=2及y=-1所得的弦长相等且不为0,则a的值是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | 2 |
12.命题“?x0∈∁RQ,x03∈Q”的否定是( )
| A. | ?x0∉∁RQ,x03∈Q | B. | ?x0∈∁RQ,x03∈Q | C. | ?x∉∁RQ,x3∈Q | D. | ?x∈∁RQ,x3∉Q |
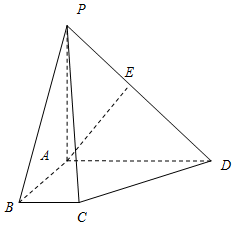 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AP⊥BC,AB=BC=1,AD=AP=2,E是PD的中点.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AP⊥BC,AB=BC=1,AD=AP=2,E是PD的中点. 如图,过椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上一点P向x轴作垂线,垂足为左焦点F,A,B分别为E的右顶点,上顶点,且AB∥OP,|AF|=$\sqrt{2}$+1.
如图,过椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上一点P向x轴作垂线,垂足为左焦点F,A,B分别为E的右顶点,上顶点,且AB∥OP,|AF|=$\sqrt{2}$+1.