题目内容
14.若不等式3x2+y2≥mx(x+y)对于?x,y∈R恒成立,则实数m的取值范围是[-6,2].分析 把y当作常数,得出关于x的一元二次不等式(3-m)x2-my•x+y2≥0恒成立,根据二次函数的性质列出不等式组解出m的范围.
解答 解:∵3x2+y2≥mx(x+y)恒成立,即(3-m)x2-my•x+y2≥0恒成立,
∴$\left\{\begin{array}{l}{3-m>0}\\{{m}^{2}{y}^{2}-4(3-m){y}^{2}≤0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{3-m>0}\\{{m}^{2}+4m-12≤0}\end{array}\right.$,解得-6≤m≤2.
故答案为[-6,2].
点评 本题考查了二次函数的性质,不等式的解法,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
11.(理)设θ为直线$x-\sqrt{3}y-1=0$的倾斜角,则$sin(θ+\frac{π}{4})$=( )
| A. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{6}+1}}{4}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ |
9.已知直角△ABC中,AB=3,AC=4,BC=5,I是△ABC的内心,P是△IBC内部(不含边界)的动点,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的取值范围是( )
| A. | ($\frac{7}{12}$,1) | B. | ($\frac{1}{3}$,1) | C. | ($\frac{1}{4}$,$\frac{7}{12}$) | D. | ($\frac{1}{4}$,1) |
19.已知函数f(x)=3sin(ωx-$\frac{π}{6}$)(ω>0)与g(x)=2cos(2x+φ)-1的图象有相同的对称轴,若$x∈[0,\frac{π}{2}]$,则f(x)的取值范围是( )
| A. | $(-\frac{3}{2},3)$ | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},\frac{3}{2}]$ | D. | [-3,3] |
6.在△ABC中,A1,B1分别是边BA,CB的中点,A2,B2分别是线段A1A,B1B的中点,…,An,Bn分别是线段${A_{n-1}}A,{B_{n-1}}B(n∈{N^*},n>1)$的中点,设数列{an},{bn}满足:向量$\overrightarrow{{B_n}{A_n}}={a_n}\overrightarrow{CA}+{b_n}\overrightarrow{CB}(n∈{N^*})$,有下列四个命题,其中假命题是( )
| A. | 数列{an}是单调递增数列,数列{bn}是单调递减数列 | |
| B. | 数列{an+bn}是等比数列 | |
| C. | 数列$\{\frac{a_n}{b_n}\}$有最小值,无最大值 | |
| D. | 若△ABC中,C=90°,CA=CB,则$|\overrightarrow{{B_n}{A_n}}|$最小时,${a_n}+{b_n}=\frac{1}{2}$ |
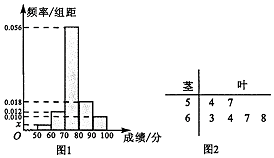 某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.
某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.