题目内容

8．设a=lg2，b=20.5，$c=cos\frac{3}{4}π$，则a，b，c按由小到大的顺序是c＜a＜b．

分析 利用指数函数与对数函数、三角函数的单调性即可得出．

解答 解：∵a=lg2∈（0，1），b=20.5＞1，$c=cos\frac{3}{4}π$＜0，
∴c＜a＜b．
故答案为：c＜a＜b．

点评 本题考查了指数函数与对数函数、三角函数的单调性，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
5．执行如图所示的程序框图，如果输出的结果为0，那么输入的x为（　　）
A．$\frac{1}{9}$B．-1或1C．-lD．l
19．已知函数f（x）=3sin（ωx-$\frac{π}{6}$）（ω＞0）与g（x）=2cos（2x+φ）-1的图象有相同的对称轴，若$x∈[0，\frac{π}{2}]$，则f（x）的取值范围是（　　）
A．$（-\frac{3}{2}，3）$B．$[-\frac{3}{2}，3]$C．$[-\frac{3}{2}，\frac{3}{2}]$D．[-3，3]
16．已知命题p与命题q，若命题：（￢p）∨q为假命题则下列说法正确是（　　）
A．p真，q真B．p假，q真C．p真，q假D．p假，q假
3．设f（x）=ex，f（x）=g（x）-h（x），且g（x）为偶函数，h（x）为奇函数，若存在实数m，当x∈[-1，1]时，不等式mg（x）+h（x）≥0成立，则m的最小值为1．
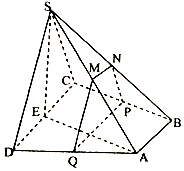13．如图，四棱锥S-ABCD中，底面ABCD为直角梯形，AB∥CD，BC⊥CD，平面SCD⊥平面ABCD，SC=SD=CD=AD=2AB，M，N分别为SA，SB的中点，E为CD中点，过M，N作平面MNPQ分别与BC，AD交于点P，Q，若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$．
（1）当t=$\frac{1}{2}$时，求证：平面SAE⊥平面MNPQ；
（2）是否存在实数t，使得二面角M-PQ-A的平面角的余弦值为$\frac{\sqrt{5}}{5}$？若存在，求出实数t的值；若不存在，说明理由．
20．执行如图所示的程序框图，则输出的n的值为（　　）
A．3B．4C．5D．6
17．如果正整数M的各位数字均不为4，且各位数字之和为6，则称M为“幸运数”，则四 位正整数中的“幸运数”共有（　　）
A．45个B．41个C．40个D．38个
18．已知函数f（x）=xln（x+1）+（$\frac{1}{2}$-a）x+2-a，a∈R．
（I）当x＞0时，求函数g（x）=f（x）+ln（x+1）+$\frac{1}{2}$x的单调区间；
（Ⅱ）当a∈Z时，若存在x≥0，使不等式f（x）＜0成立，求a的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网