题目内容
5.已知函数f(x)=$\frac{x}{cosx}$的定义域为(-$\frac{π}{2}$,$\frac{π}{2}$),当|xi|<$\frac{π}{2}$时(i=1,2,3),f(x1)+f(x2)≥0,f(x2)+f(x3)≥0,f(x3)+f(x1)≥0,则下列结论正确的是( )| A. | x1+x2+x3>0 | B. | x1+x2+x3<0 | C. | f(x1+x2+x3)≥0 | D. | f(x1+x2+x3)≤0 |
分析 由函数的导函数得知在x∈(0,$\frac{π}{2}$)是单调递增的,再由奇偶性得到在x∈(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增,通过单调性与奇偶性相结合得到x1+x2+x3≥0,所以对应的函数值可以确定.
解答 解:∵函数f(x)=$\frac{x}{cosx}$的定义域为(-$\frac{π}{2}$,$\frac{π}{2}$),且f(-x)=-f(x)
∴f(x)为奇函数
∵f′(x)=$\frac{cosx+xsinx}{(cosx)^{2}}$
∴f(x)在x∈(0,$\frac{π}{2}$)是单调递增的.
∴f(x)在x∈(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增.
∵f(x1)+f(x2)≥0,
∴f(x1)≥-f(x2)≥0,
∴f(x1)≥f(-x2)≥0,
∴x1≥-x2,
同理可得:x2≥-x3,x3≥-x1
∴x1+x2≥0,x2+x3≥0,x3+x1≥0
∴x1+x2+x3≥0,
∴f(x1+x2+x3)≥f(0)=0,
故选C
点评 本题考查由函数的导函数和奇偶性得到单调性,从而得到x1+x2+x3≥0,所以对应的函数值可以确定.

练习册系列答案
相关题目
10.已知双曲线C:$\frac{x^2}{16}-\frac{y^2}{b^2}=1({b>0})$的右焦点与抛物线y2=20x的焦点重合,则双曲线C的渐近线方程为( )
| A. | 4x±3y=0 | B. | 3x±4y=0 | C. | 16x±9y=0 | D. | 9x±16y=0 |
17.双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点为F(c,0),若圆C:(x-c)2+y2=4a2与双曲线E的渐近线相切,则E的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
14.过点E(1,0)作两条互相垂直的直线交抛物线y2=4x于点A、B、C、D,且M、N分别是AB、CD的中点,则三角形EMN面积的最小值为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | 4 |
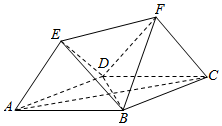 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.