题目内容
17.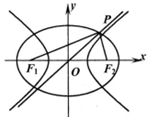 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )| A. | e22=$\frac{1+{{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | B. | e22=$\frac{{2{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | ||
| C. | e22=$\frac{1-{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ | D. | e22=$\frac{{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ |
分析 设椭圆及双曲线方程,由曲线共焦点,则c2+b12=a12,a22+b22=c2,求得双曲线的渐近线方程,代入椭圆方程,求得P点坐标,由直角三角形的性质,即可求得丨OP丨=c,利用勾股定理及椭圆及双曲线的性质即可求得答案.
解答 解:设椭圆的方程为:$\frac{{x}^{2}}{{a}_{1}^{2}}+\frac{{y}^{2}}{{b}_{1}^{2}}=1$,双曲线的方程为:$\frac{{x}^{2}}{{a}_{2}^{2}}-\frac{{y}^{2}}{{b}_{2}^{2}}=1$,P(x,y),
由题意可知:c2+b12=a12,a22+b22=c2,
双曲线的渐近线方程:y=±$\frac{{b}_{2}}{{a}_{2}}$x,
将渐近线方程代入椭圆方程:解得:x2=$\frac{{a}_{1}^{2}{a}_{2}^{2}{b}_{1}^{2}}{{a}_{2}^{2}{b}_{1}^{2}+{a}_{1}^{2}{b}_{2}^{2}}$,y2=$\frac{{a}_{1}^{2}{b}_{2}^{2}{b}_{1}^{2}}{{a}_{2}^{2}{b}_{1}^{2}+{a}_{1}^{2}{b}_{2}^{2}}$,
由PF1⊥PF2,
∴丨OP丨=$\frac{1}{2}$丨F1F2丨=c,
∴x2+y2=c2,
代入整理得:a14+a22c2=2a12c2,
两边同除以c4,由椭圆及双曲线的离心率公式可知:e1=$\frac{c}{{a}_{1}}$,e2=$\frac{c}{{a}_{2}}$,
整理得:e22=$\frac{{e}_{1}^{4}}{2{e}_{1}^{2}-1}$,
故选D.
点评 本题考查椭圆及双曲线的标准方程及简单几何性质,考查直角三角形的性质及勾股定理的应用,考查计算能力,属于中档题.

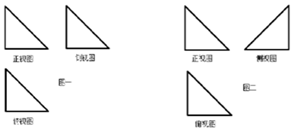 小明在解决三视图还原问题时,错把图一的三视图看成图二的三视图,假设图一所对应几何体中最大的面积为S1,图二所对应几何体中最大面的面积为S2,三视图中所有三角形均为全等的等腰直角三角形,则$\frac{{S}_{1}}{{S}_{2}}$=( )
小明在解决三视图还原问题时,错把图一的三视图看成图二的三视图,假设图一所对应几何体中最大的面积为S1,图二所对应几何体中最大面的面积为S2,三视图中所有三角形均为全等的等腰直角三角形,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | 1 | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
