题目内容
11．已知曲线C1的参数方程为$\left\{\begin{array}{l}x=acosθ\\ y=bsinθ\end{array}\right.$（a＞b＞0，θ为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=r（r＞0）．（1）求曲线C1的普通方程与曲线C2的直角坐标方程，并讨论两曲线公共点的个数；
（2）若b＜r＜a，求由两曲线C1与C2交点围成的四边形面积的最大值．
分析 （1）方程化为普通方程，即可讨论两曲线公共点的个数；
（2）若b＜r＜a，两曲线均关于x，y轴、原点对称，四边形也关于x，y轴、原点对称，即可求由两曲线C1与C2交点围成的四边形面积的最大值．
解答 解：（1）曲线C1的参数方程为$\left\{\begin{array}{l}x=acosθ\\ y=bsinθ\end{array}\right.$（a＞b＞0，θ为参数），普通方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1，
曲线C2的极坐标方程为ρ=r（r＞0），直角坐标方程为x2+y2=r2，
r=a或b时，两曲线有两个公共点；
b＜r＜a时，两曲线有四个公共点；
0＜r＜b或r＞a时，两曲线无公共点；
（2）两曲线均关于x，y轴、原点对称，
∴四边形也关于x，y轴、原点对称，
设四边形位于第一象限的点为（acosθ，bsinθ），
则四边形的面积为S=4acosθ•bsinθ=2absin2θ≤2ab，
当且仅当sin2θ=1，即θ=45°时，等号成立．
点评 本题考查参数方程、极坐标方程与普通方程的转化，考查三角函数知识的运用，属于中档题．
练习册系列答案
相关题目
1．
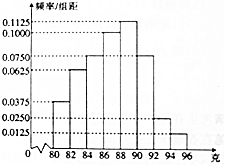某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量（单位：克）绘制的频率分布直方图，样本数据分8组，分别为[80，82），[82，84），[84，86），[86，88），[88，90），[90，92），[92，94），[94，96]，则样本的中位数在（ ）
某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量（单位：克）绘制的频率分布直方图，样本数据分8组，分别为[80，82），[82，84），[84，86），[86，88），[88，90），[90，92），[92，94），[94，96]，则样本的中位数在（ ）| A． | 第3组 | B． | 第4组 | C． | 第5组 | D． | 第6组 |
2．已知x，y满足$\left\{\begin{array}{l}{y≥x}&{\;}\\{x+y≤2}&{\;}\\{x≥a}&{\;}\end{array}\right.$，且z=2x-y的最大值是最小值的-2倍，则a=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | -$\frac{2}{3}$ |
19．甲乙二人争夺一场围棋比赛的冠军，若比赛为“三局两胜”制，甲在每局比赛中获胜的概率均为$\frac{2}{3}$，且各局比赛结果相互独立，则在甲获得冠军的情况下，比赛进行了三局的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{5}$ | C． | $\frac{2}{3}$ | D． | $\frac{4}{5}$ |
16．某几何体的三视图如图所示，则其表面积为（ ）
| A． | $\frac{2π}{3}$ | B． | $\frac{4π}{3}$ | C． | 2π | D． | 3π |