题目内容
12．当x＞0时，函数f（x）=（aex+b）（x-2）单调递增，且函数y=f（x-1）的图象关于直线x=1对称，则使得f（2-m）＞0成立的m的取值范围是（ ）| A． | {m|m＜-2或m＞2} | B． | {m|-2＜m＜2} | C． | {m|m＜0或m＞4} | D． | {m|0＜m＜4} |
分析 根据函数的对称性得到函数f（x）是偶函数，根据f（2）=f（-2）=0，问题转化为|2-m|＞2，求出m的范围即可．
解答 解：函数y=f（x-1）的图象关于直线x=1对称，
即函数y=f（x）的图象关于y轴对称，
函数f（x）是偶函数，
而f（2）=0，故x＞2时，f（x）＞0，x＜-2时，f（x）＞0，
故f（2-m）＞0，即|2-m|＞2，解得：m＞4或m＜0，
故选：C．
点评 本题考查了函数的对称性问题，考查转化思想以及函数的单调性，是一道中档题．
练习册系列答案
相关题目
7．
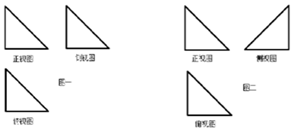小明在解决三视图还原问题时，错把图一的三视图看成图二的三视图，假设图一所对应几何体中最大的面积为S1，图二所对应几何体中最大面的面积为S2，三视图中所有三角形均为全等的等腰直角三角形，则$\frac{{S}_{1}}{{S}_{2}}$=（ ）
小明在解决三视图还原问题时，错把图一的三视图看成图二的三视图，假设图一所对应几何体中最大的面积为S1，图二所对应几何体中最大面的面积为S2，三视图中所有三角形均为全等的等腰直角三角形，则$\frac{{S}_{1}}{{S}_{2}}$=（ ）| A． | 1 | B． | $\frac{\sqrt{6}}{6}$ | C． | $\frac{\sqrt{6}}{2}$ | D． | $\frac{\sqrt{6}}{3}$ |
4．已知角θ的终边过点（2sin2$\frac{π}{8}$-1，a），若sinθ=2$\sqrt{3}$sin$\frac{13π}{12}$cos$\frac{π}{12}$，则实数a等于（ ）
| A． | -$\sqrt{6}$ | B． | -$\frac{\sqrt{6}}{2}$ | C． | ±$\sqrt{6}$ | D． | ±$\frac{\sqrt{6}}{2}$ |
1．
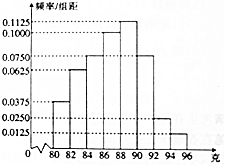某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量（单位：克）绘制的频率分布直方图，样本数据分8组，分别为[80，82），[82，84），[84，86），[86，88），[88，90），[90，92），[92，94），[94，96]，则样本的中位数在（ ）
某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量（单位：克）绘制的频率分布直方图，样本数据分8组，分别为[80，82），[82，84），[84，86），[86，88），[88，90），[90，92），[92，94），[94，96]，则样本的中位数在（ ）| A． | 第3组 | B． | 第4组 | C． | 第5组 | D． | 第6组 |
2．已知x，y满足$\left\{\begin{array}{l}{y≥x}&{\;}\\{x+y≤2}&{\;}\\{x≥a}&{\;}\end{array}\right.$，且z=2x-y的最大值是最小值的-2倍，则a=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | -$\frac{2}{3}$ |