题目内容
3.已知G,N,P在△ABC所在平面内,a,b,c分别为角A,B,C所对的边,且分别满足$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,sin2A•$\overrightarrow{NA}$+sin2B•$\overrightarrow{NB}$+sin2C•$\overrightarrow{NC}$=$\overrightarrow{0}$,a$\overrightarrow{PA}$+b$\overrightarrow{PB}$+c$\overrightarrow{PC}$=$\overrightarrow 0$,则点G,N,P依次是△ABC的( )| A. | 重心,外心,内心 | B. | 重心,垂心,内心 | C. | 重心,垂心,外心 | D. | 内心,外心,重心 |
分析 假设三角形内一点O分别为内心,外心,重心,利用结论S△BOC$•\overrightarrow{OA}$+S△AOC$•\overrightarrow{OB}$+S△AOB$•\overrightarrow{OC}$=$\overrightarrow{0}$推导变形验证.
解答 解:(1)取AC中点D,连结GD,则$\overrightarrow{GA}+\overrightarrow{GC}$=2$\overrightarrow{GD}$,∵$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,∴$\overrightarrow{GA}+\overrightarrow{GC}$=-$\overrightarrow{GB}$.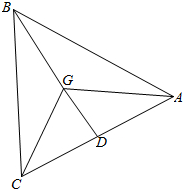
∴2$\overrightarrow{GD}$=-$\overrightarrow{GC}$.∴G在△ABC的中线BD上,同理可得G在其它两边的中线上,
∴G是△ABC的重心.
(2)∵S△BCN•$\overrightarrow{NA}$+S△ACN•$\overrightarrow{NB}$+S△ABN$•\overrightarrow{NC}$=$\overrightarrow{0}$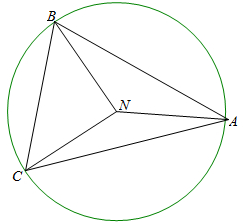
∴当N是△ABC的外心时,设外接圆半径为r,
则S△BCN=$\frac{1}{2}sin∠$BNC•r2=$\frac{{r}^{2}}{2}$sin2∠BAC,
S△ACN=$\frac{1}{2}$sin∠ACN•r2=$\frac{{r}^{2}}{2}$sin2∠ABC,
S△ABN=$\frac{1}{2}$sin∠ANB•r2=$\frac{{r}^{2}}{2}$sin2∠ACB.
∴sin2∠BAC•$\overrightarrow{NA}$+sin2∠ABC•$\overrightarrow{NB}$+sin2∠ACB•$\overrightarrow{NC}$=$\overrightarrow{0}$.
(3)延长CP交AB于D,则$\overrightarrow{PA}=\overrightarrow{PD}+\overrightarrow{DA}$,$\overrightarrow{PB}=\overrightarrow{PD}+\overrightarrow{DB}$,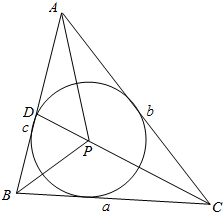
∵a$\overrightarrow{PA}$+b$\overrightarrow{PB}$+c$\overrightarrow{PC}$=$\overrightarrow 0$,
∴a($\overrightarrow{PD}+\overrightarrow{DA}$)+b($\overrightarrow{PD}+\overrightarrow{DB}$)+c$\overrightarrow{PC}$=$\overrightarrow{0}$,
设$\overrightarrow{PD}$=k$\overrightarrow{PC}$,则(ka+kb+c)$\overrightarrow{PC}$+( a$\overrightarrow{DA}$+b$\overrightarrow{DB}$)=$\overrightarrow{0}$,
∵$\overrightarrow{DA}$与$\overrightarrow{DB}$共线,$\overrightarrow{PC}$与$\overrightarrow{DA}$,$\overrightarrow{DB}$不共线,
∴ka+kb+c=0,a$\overrightarrow{DA}$+b$\overrightarrow{DB}$=$\overrightarrow{0}$,
∴$\frac{DA}{DB}$=-$\frac{b}{a}$,
∴CD为∠ACB的平分线,同理可证其它的两条也是角平分线.
∴P是△ABC的内心.
综上,G是三角形的重心,N是三角形的外心,P是三角形的内心.
故选:A.
点评 本题考查了平面向量的基本定理,记住三角形内一点的一般结论是解题关键,属于中档题.

| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
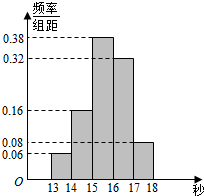 某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.
某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.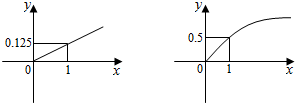 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).