题目内容
已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2
(1)判断f(x)的奇偶性;
(2)判断f(x)在R上的单调性;
(3)求f(x)在区间[-3,3]上的值域;
(4)若任意x∈R,不等式f(ax2)-2f(x)<f(x)+4恒成立,求a的取值范围.
(1)判断f(x)的奇偶性;
(2)判断f(x)在R上的单调性;
(3)求f(x)在区间[-3,3]上的值域;
(4)若任意x∈R,不等式f(ax2)-2f(x)<f(x)+4恒成立,求a的取值范围.
考点:抽象函数及其应用,函数单调性的判断与证明,函数奇偶性的判断,函数恒成立问题
专题:函数的性质及应用
分析:(1)可根据函数奇偶性的定义进行证明,应由条件先得到f(0)=0后,再利用条件f(x1+x2)=f(x1)+f(x2)中x1、x2的任意性,可使结论得证.
(2)可根据函数单调性的定义进行论证,考虑证明过程中如何利用题设条件.
(3)由(2)的结论可知f(-3)、f(3)分别是函数y=f(x)在[-3,3]上的最大值与最小值,可得所求值域.
(4)根据函数的奇偶性、单调性可把f(ax2)+2f(-x)<f(x)+f(-2)转化为具体不等式恒成立,利用数形结合即可得到关于a的限制条件,解出即可
(2)可根据函数单调性的定义进行论证,考虑证明过程中如何利用题设条件.
(3)由(2)的结论可知f(-3)、f(3)分别是函数y=f(x)在[-3,3]上的最大值与最小值,可得所求值域.
(4)根据函数的奇偶性、单调性可把f(ax2)+2f(-x)<f(x)+f(-2)转化为具体不等式恒成立,利用数形结合即可得到关于a的限制条件,解出即可
解答:
解:(1)f(x)为奇函数,
由f(x+y)=f(x)+f(y),得f(x-x)=f(x)+f(-x)
即f(x)+f(-x)=f(0),而令x=y=0可得f(0)=0
∴f(-x)=-f(x),即函数y=f(x)是奇函数
(2)f(x)在R上单调递减,
任取x1、x2∈R,且x1<x2,f(x2)=f[x1+(x2-x1)],
于是由题设条件f(x+y)=f(x)+f(y)可知f(x2)=f(x1)+f(x2-x1).
∵x2>x1,
∴x2-x1>0.
∴f(x2-x1)<0.
∴f(x2)=f(x1)+f(x2-x1)<f(x1).
故函数y=f(x)是单调减函数.
(3)由函数y=f(x)是R上的单调减函数,
∴y=f(x)在[-3,3]上也为单调减函数.
∴y=f(x)在[-3,3]上的最大值为f(-3),最小值为f(3).
∴f(3)=f(1+2)=f(1)+f(2)=3f(1)=-6.
∴f(-3)=-f(3)=6
因此,函数y=f(x)在[-3,3]上的值域为[-6,6].
(4)令x=1,y=1得f(2)=f(1+1)=f(1)+f(1)=-2-2=-4,
∵f(ax2)-2f(x)<f(x)+4,
∴f(ax2)-4<2f(x)+f(x),
∴f(ax2)+f(2)<f(3x),
∴f(ax2+2)<f(3x),
又函数y=f(x)是R上的单调减函数,
∴ax2+2>3x,
即ax2-3x+2>0恒成立,
①当a=0时不成立,
②当a≠0时,有a>0且△<0,即
解得a>
,
故a的取值范围为(
,+∞)
由f(x+y)=f(x)+f(y),得f(x-x)=f(x)+f(-x)
即f(x)+f(-x)=f(0),而令x=y=0可得f(0)=0
∴f(-x)=-f(x),即函数y=f(x)是奇函数
(2)f(x)在R上单调递减,
任取x1、x2∈R,且x1<x2,f(x2)=f[x1+(x2-x1)],
于是由题设条件f(x+y)=f(x)+f(y)可知f(x2)=f(x1)+f(x2-x1).
∵x2>x1,
∴x2-x1>0.
∴f(x2-x1)<0.
∴f(x2)=f(x1)+f(x2-x1)<f(x1).
故函数y=f(x)是单调减函数.
(3)由函数y=f(x)是R上的单调减函数,
∴y=f(x)在[-3,3]上也为单调减函数.
∴y=f(x)在[-3,3]上的最大值为f(-3),最小值为f(3).
∴f(3)=f(1+2)=f(1)+f(2)=3f(1)=-6.
∴f(-3)=-f(3)=6
因此,函数y=f(x)在[-3,3]上的值域为[-6,6].
(4)令x=1,y=1得f(2)=f(1+1)=f(1)+f(1)=-2-2=-4,
∵f(ax2)-2f(x)<f(x)+4,
∴f(ax2)-4<2f(x)+f(x),
∴f(ax2)+f(2)<f(3x),
∴f(ax2+2)<f(3x),
又函数y=f(x)是R上的单调减函数,
∴ax2+2>3x,
即ax2-3x+2>0恒成立,
①当a=0时不成立,
②当a≠0时,有a>0且△<0,即
|
解得a>
| 9 |
| 8 |
故a的取值范围为(
| 9 |
| 8 |
点评:本题考查抽象函数 的奇偶性、单调性及其应用,考查函数恒成立问题,考查学生分析问题解决问题的能力,属中档题.

练习册系列答案
相关题目
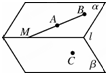 如图,α∩β=l,A,B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
如图,α∩β=l,A,B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )| A、点A | B、点B |
| C、点C但不过点M | D、点C和点M |
已知F1,F2是双曲线
-
=1(a>0,b>0)的焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、4+2
| ||||
B、
| ||||
C、
| ||||
D、
|
