题目内容
20. 如图,在平面直角坐标系xOy中,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,直线y=$\frac{b}{2}$与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是$\frac{\sqrt{6}}{3}$.
如图,在平面直角坐标系xOy中,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,直线y=$\frac{b}{2}$与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是$\frac{\sqrt{6}}{3}$.
分析 设右焦点F(c,0),将y=$\frac{b}{2}$代入椭圆方程求得B,C的坐标,运用两直线垂直的条件:斜率之积为-1,结合离心率公式,计算即可得到所求值.方法二、运用向量的数量积的性质,向量垂直的条件:数量积为0,结合离心率公式计算即可得到所求.
解答 解:设右焦点F(c,0),
将y=$\frac{b}{2}$代入椭圆方程可得x=±a$\sqrt{1-\frac{{b}^{2}}{4{b}^{2}}}$=±$\frac{\sqrt{3}}{2}$a,
可得B(-$\frac{\sqrt{3}}{2}$a,$\frac{b}{2}$),C($\frac{\sqrt{3}}{2}$a,$\frac{b}{2}$),
由∠BFC=90°,可得kBF•kCF=-1,
即有$\frac{\frac{b}{2}}{-\frac{\sqrt{3}}{2}a-c}$•$\frac{\frac{b}{2}}{\frac{\sqrt{3}}{2}a-c}$=-1,
化简为b2=3a2-4c2,
由b2=a2-c2,即有3c2=2a2,
由e=$\frac{c}{a}$,可得e2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{2}{3}$,
可得e=$\frac{\sqrt{6}}{3}$,
另解:设右焦点F(c,0),
将y=$\frac{b}{2}$代入椭圆方程可得x=±a$\sqrt{1-\frac{{b}^{2}}{4{b}^{2}}}$=±$\frac{\sqrt{3}}{2}$a,
可得B(-$\frac{\sqrt{3}}{2}$a,$\frac{b}{2}$),C($\frac{\sqrt{3}}{2}$a,$\frac{b}{2}$),
$\overrightarrow{FB}$=(-$\frac{\sqrt{3}}{2}$a-c,$\frac{b}{2}$),$\overrightarrow{FC}$=($\frac{\sqrt{3}}{2}$a-c,$\frac{b}{2}$),
$\overrightarrow{FB}$•$\overrightarrow{FC}$=0,则c2-$\frac{3}{4}$a2十$\frac{1}{4}$b2=0,
因为b2=a2-c2,代入得3c2=2a2,
由e=$\frac{c}{a}$,可得e2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{2}{3}$,
可得e=$\frac{\sqrt{6}}{3}$.
故答案为:$\frac{\sqrt{6}}{3}$.
点评 本题考查椭圆的离心率的求法,注意运用两直线垂直的条件:斜率之积为-1,考查化简整理的运算能力,属于中档题.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案| A. | 1个 | B. | 2个 | C. | 4个 | D. | 3个 |
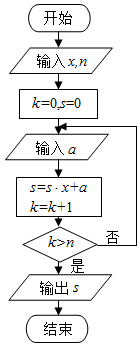 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )