题目内容
8.行列式$|{\begin{array}{l}a&b\\ c&d\end{array}}|$(a、b、c、d∈{-1,1,2})所有可能的值中,最小值为-6.分析 利用二阶行列式展开式法则求解.
解答 解:∵行列式$|{\begin{array}{l}a&b\\ c&d\end{array}}|$=ad-bc,
a、b、c、d∈{-1,1,2},
∴所有可能的值中,当a,d分别取-1,2,b和c取2时,
行列式最小值为:$|{\begin{array}{l}a&b\\ c&d\end{array}}|$=ad-bc=-2-4=-6.
故答案为:-6.
点评 本题考查二阶行列式的最小值的求法,是基础题,解题时要注意二阶行列式展开法则的合理运用.

练习册系列答案
相关题目
18.函数$f(x)=\left\{\begin{array}{l}2{x^3}+3{x^2}+1(x≤0)\\{e^{ax}}(x>0)\end{array}\right.$在[-2,3]上的最大值为2,则实数a的取值范围是( )
| A. | $[\frac{1}{3}ln2,+∞)$ | B. | $[0,\frac{1}{3}ln2]$ | C. | (-∞,0] | D. | $(-∞,\frac{1}{3}ln2]$ |
19.设等差数列{an}的前n项和为Sn,其公差为-1,若S1,S2,S4成等比数列,则a1=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
16.已知{an}为等差数列,a1+a3=2,则a2等于( )
| A. | -1 | B. | 1 | C. | 3 | D. | 7 |
18.如图,在长方体ABCD-A1B1C1D1中,AA1=2AB,AB=BC,则下列结论中正确的是( )
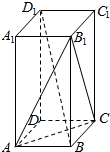

| A. | BD1∥B1C | B. | A1D1∥平面AB1C | C. | BD1⊥AC | D. | BD1⊥平面AB1C |