题目内容
已知向量
=(2sinθ,sinθ+cosθ),
=(cosθ,-2-m),函数f(θ)=
•
(1)当m=1时,求f(
)的值;
(2)若θ∈[-
,
],问是否存在实数m的值使得f(θ)的最小值为-
,若存在,求出实数m的值;若不存在,说明理由.
| m |
| n |
| m |
| n |
(1)当m=1时,求f(
| π |
| 4 |
(2)若θ∈[-
| π |
| 4 |
| π |
| 4 |
| 3 |
| 4 |
考点:平面向量数量积的运算,三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:(1)由向量的数量积的坐标表示,代入m=1,由特殊角的三角函数值化简即可得到;
(2)假设存在实数m的值使得f(θ)的最小值为-
,令t=sinθ+cosθ,由θ∈[-
,
],求得t的范围,两边平方可得2sinθcosθ=t2-1,转化为二次函数的最值求法,通过对称轴和区间的关系,即可求得最小值,进而判断是否存在.
(2)假设存在实数m的值使得f(θ)的最小值为-
| 3 |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答:
解:(1)向量
=(2sinθ,sinθ+cosθ),
=(cosθ,-2-m),
则函数f(θ)=
•
=2sinθcosθ-(2+m)(sinθ+cosθ),
当m=1时,f(θ)=2sinθcosθ-3(sinθ+cosθ);
则f(
)=2sin
cos
-3(sin
+cos
)=1-3
;
(2)假设存在实数m的值使得f(θ)的最小值为-
,
f(θ)=2sinθcosθ-(2+m)(sinθ+cosθ),
令t=sinθ+cosθ=
sin(θ+
),
由θ∈[-
,
],则θ+
∈[0,
],即有t∈[0,2],
由t2=1+2sinθcosθ,得2sinθcosθ=t2-1,
则f(θ)=t2-1-(2+m)t=(t-
)2-1-
,
由于最小值点可能在端点处和顶点处,
且-1-
<-1,则最小值不可能在顶点处,
若区间[0,2]为增区间即
≤0,则t=0取得最小值-1,不成立;
若区间[0,2]为减区间即
≥2,则t=2取得最小值3-2(2+m)=-
,
解得m=-
,不成立.
综上可得,不存在实数m的值使得f(θ)的最小值为-
.
| m |
| n |
则函数f(θ)=
| m |
| n |
当m=1时,f(θ)=2sinθcosθ-3(sinθ+cosθ);
则f(
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 2 |
(2)假设存在实数m的值使得f(θ)的最小值为-
| 3 |
| 4 |
f(θ)=2sinθcosθ-(2+m)(sinθ+cosθ),
令t=sinθ+cosθ=
| 2 |
| π |
| 4 |
由θ∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
由t2=1+2sinθcosθ,得2sinθcosθ=t2-1,
则f(θ)=t2-1-(2+m)t=(t-
| 2+m |
| 2 |
| (m+2)2 |
| 4 |
由于最小值点可能在端点处和顶点处,
且-1-
| (m+2)2 |
| 4 |
若区间[0,2]为增区间即
| m+2 |
| 2 |
若区间[0,2]为减区间即
| m+2 |
| 2 |
| 3 |
| 4 |
解得m=-
| 1 |
| 8 |
综上可得,不存在实数m的值使得f(θ)的最小值为-
| 3 |
| 4 |
点评:本题考查向量的数量积的坐标表示,主要考查三角函数的恒等变换和求值,考查运算能力,注意二次函数的最值求法是解题关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
已知函数f(x)=x2lnx-ax3-x2+x,若?λ∈R使λf(x)-xf(λ)≤0恒成立,则实数a的取值范围为( )
A、(0,
| ||
B、(0,
| ||
C、(0,
| ||
D、(0,
|
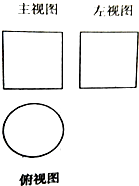 如图一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,则该几何体的侧面积为
如图一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,则该几何体的侧面积为