题目内容
20.已知关于x不等式x2-mx-6m<0的解集为{x|-3<x<6},则m=3.分析 利用不等式x不等式x2-mx-6m<0的解集为{x|-3<x<6},得到二次不等式所对应的方程的根,求方程的根即可得到m的值.
解答 解:∵关于x的不等式x2-mx-6m<0的解集为{x|-3<x<6},
∴-3,6为方程x2-mx-6m=0的两个根,由此可得-3+6=m,解的m=3.
故答案为:3.
点评 本题考查了一元二次不等式的解法,考查了“三个二次”的结合,是基础题.

练习册系列答案
相关题目
11.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右焦点为F1,F2.A,B为顶点,以线段F1F2为直径的圆交双曲线的一条渐近线bx-ay=0于M,N两点,且∠MAB=30°,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{21}}}{3}$ | B. | 2 | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{5}{3}$ |
12. 如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
 如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )| A. | 1:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{2}$:2 | D. | 1:2 |
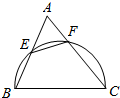 如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.
如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.
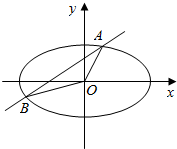 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列.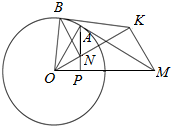 如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P.
如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P.