题目内容
3.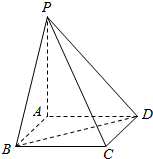 已知PA垂直于矩形ABCD所在平面,PA=3,AB=1,BC=$\sqrt{3}$.
已知PA垂直于矩形ABCD所在平面,PA=3,AB=1,BC=$\sqrt{3}$.(1)求二面角P-BD-A的正切值;
(2)求二面角B-PD-A的正切值.
分析 (1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,求出平面PBD的法向量和平面ABD的法向量,利用向量法能求出二面角P-BD-A的正切值.
(2)求出平面PBD的法向量和平面PDA的法向量,利用向量法能求出二面角B-PD-A的正切值.
解答  解:(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
解:(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
由已知得P(0,0,3),B(1,0,0),D(0,$\sqrt{3}$,0),A(0,0,0),
$\overrightarrow{PB}$=(1,0,-3),$\overrightarrow{PD}$=(0,$\sqrt{3}$,-3),
设平面PBD的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=x-3z=0}\\{\overrightarrow{n}•\overrightarrow{PD}=\sqrt{3}y-3z=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=(3,$\sqrt{3}$,1),
又平面ABD的法向量$\overrightarrow{m}$=(0,0,1),
设二面角P-BD-A的平面角为θ,
则cosθ=|cos<$\overrightarrow{n},\overrightarrow{m}$>|=|$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}|•|\overrightarrow{m}|}$|=|$\frac{1}{\sqrt{13}}$|=$\frac{\sqrt{13}}{13}$,
∴tanθ=2$\sqrt{3}$,即二面角P-BD-A的正切值为2$\sqrt{3}$.
(2)平面PBD的法向量$\overrightarrow{n}$=(3,$\sqrt{3}$,1),平面PDA的法向量$\overrightarrow{p}$=(1,0,0),
设二面角B-PD-A的平面角为α,
则cosα=|cos<$\overrightarrow{n},\overrightarrow{p}$>|=|$\frac{\overrightarrow{n}•\overrightarrow{p}}{|\overrightarrow{n}|•|\overrightarrow{p}|}$|=|$\frac{3}{\sqrt{13}}$|=$\frac{3\sqrt{13}}{13}$,
∴tanα=$\frac{2}{3}$,即二面角B-PD-A的正切值为$\frac{2}{3}$.
点评 本题考查二面角的正切值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

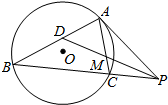 如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )
如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 5$\sqrt{2}$ |
| A. | $\frac{{\sqrt{21}}}{3}$ | B. | 2 | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{5}{3}$ |
 如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )| A. | 1:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{2}$:2 | D. | 1:2 |
| A. | (-∞,-1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
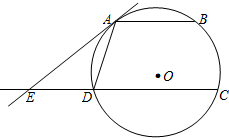 在圆O中,AB,CD是互相平行的两条弦,直线AE与圆O相切于点A,且与CD的延长线交于点E,求证:AD2=AB•ED.
在圆O中,AB,CD是互相平行的两条弦,直线AE与圆O相切于点A,且与CD的延长线交于点E,求证:AD2=AB•ED.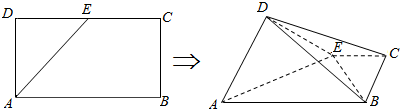
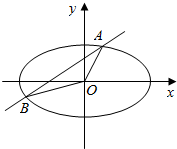 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列.