题目内容
6．已知两定点A（-2，1），B（1，3），动点P在直线x-y+1=0上，当|PA|+|PB|取最小值时，这个最小值为（ ）| A． | $\sqrt{5}$ | B． | 3 | C． | $\sqrt{13}$ | D． | $\sqrt{17}$ |
分析 设点A（-2，1）关于直线x-y+1=0的对称点A′（m，n）．利用轴对称的性质可得A′的坐标．连接A′B与直线相交于点P，则|PA|+|PB|的最小值为|A′B|．利用两点间的距离公式即可得出|PA|+|PB|的最小值．
解答 解：设点A（-2，1）关于直线x-y+1=0的对称点A′（m，n）．
则$\left\{\begin{array}{l}{\frac{-2+m}{2}-\frac{1+n}{2}+1=0}\\{\frac{n-1}{m+2}=-1}\end{array}\right.$，
解得m=0，n=-1，
连接A′B与直线相交于点P，则|PA|+|PB|的最小值为|A′B|=$\sqrt{（1-0）^{2}+（3+1）^{2}}$=$\sqrt{17}$．
故选：D．
点评 本题考查了最小值问题转化为轴对称问题，考查了相互垂直的直线斜率之间的关系和中点坐标公式，属于中档题．
练习册系列答案
相关题目
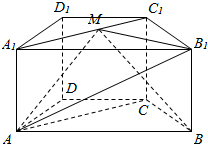在四棱柱ABCD-A1B1C1D1中，底面ABCD为梯形，AB∥CD，AD=DC=CB=1，∠ABC=$\frac{π}{3}$，对角面A1ACC1为矩形，平面A1ACC1⊥平面ABCD，CC1=1．
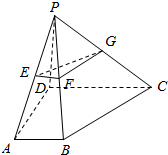如图，四棱锥P-ABCD的底面为直角梯形，且∠BAD=∠ADC=90°，E，F，G分别为PA，PB，PC的中点，直线PB⊥平面EFG，AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1．
11．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左，右焦点为F1，F2．A，B为顶点，以线段F1F2为直径的圆交双曲线的一条渐近线bx-ay=0于M，N两点，且∠MAB=30°，则双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{21}}}{3}$ | B． | 2 | C． | $\frac{{\sqrt{6}}}{2}$ | D． | $\frac{5}{3}$ |
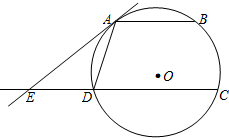在圆O中，AB，CD是互相平行的两条弦，直线AE与圆O相切于点A，且与CD的延长线交于点E，求证：AD2=AB•ED．
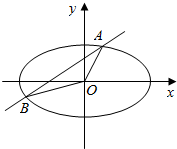已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴是短轴的两倍，点P（$\sqrt{3}$，$\frac{1}{2}$）在椭圆上．不过原点的直线l与椭圆相交于A、B两点，设直线OA、l、OB的斜率分别为k1、k、k2，且k1、k、k2恰好构成等比数列．