题目内容
15．设P是双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{9}$=1上一点，该双曲线的一条渐近线方程是3x+4y=0，F1，F2分别是双曲线的左、右焦点，若|PF1|=10，则|PF2|等于18或2．分析 根据双曲线的渐近线方程可求得a和b的关系，进而求得a，根据双曲线定义可知∴|PF1|-|PF2|=2a或|PF2|-|PF1|=2a，进而求得答案．
解答 解：∵双曲线的一条渐近线方程是3x+4y=0，b=3，
∴$\frac{3}{a}$=$\frac{3}{4}$，∴a=4，
∴|PF1|-|PF2|=2a=8或|PF2|-|PF1|=2a=8
∴|PF2|=2或18，
故答案为：18或2．
点评 本题主要考查了双曲线的简单性质，属基础题．
练习册系列答案
相关题目
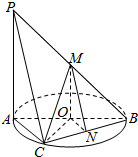如图，AB为圆O的直径，点C在圆周上（异于点A，B），直线PA垂直于圆O所在的平面，点M，N分别为线段PB，BC的中点，有以下三个命题：