题目内容
若函数f(x)=ax2-(a+2)x+1在区间(-2,-1)上恰有一个零点,则实数a的取值范围是 .
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:由题意,分a的取值讨论,从而求a的取值范围.
解答:
解:①当a=0时,-2x+1=0,故x=
;
②当a<0时,函数f(x)=ax2-(a+2)x+1的零点一正一负,
故f(-2)•f(-1)=(6a+5)(2a+3)<0,
故-
<a<-
;
③当a>0时,ax2-(a+2)x+1=0的两根为正值,
故函数f(x)=ax2-(a+2)x+1在区间(-2,-1)上没有零点,
综上所述,-
<a<-
.
故答案为:-
<a<-
.
| 1 |
| 2 |
②当a<0时,函数f(x)=ax2-(a+2)x+1的零点一正一负,
故f(-2)•f(-1)=(6a+5)(2a+3)<0,
故-
| 3 |
| 2 |
| 5 |
| 6 |
③当a>0时,ax2-(a+2)x+1=0的两根为正值,
故函数f(x)=ax2-(a+2)x+1在区间(-2,-1)上没有零点,
综上所述,-
| 3 |
| 2 |
| 5 |
| 6 |
故答案为:-
| 3 |
| 2 |
| 5 |
| 6 |
点评:本题考查了函数的零点与方程的根的关系应用,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
求满足2x(2sinx-
)≥0,x∈(0,2π)的角α的集合( )
| 3 |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
2cos230°-1的值为( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
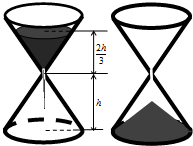 沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的
沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的