题目内容
20.某种病毒经30分钟繁殖为原来的2倍,且已知病毒的繁殖规律为y=ekx(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则经过5小时,1个病毒能繁殖为1024个.分析 由题意可得,在函数y=ekt中,当t=1时,y=4,从而可求k,然后利用所求函数解析式可求当t=5时的函数值.
解答 解:∵某个病毒经30分钟繁殖为原来的2倍,
∴在函数y=ekt中,当t=1时,y=4
∴4=ek,即k=ln4,
当a=5时,ekt=e5ln4=45=1024,
故答案为:1024.
点评 本题主要考查了指数函数在求解函数值中的应用,解题的关键是根据已知求出函数解析式.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
10.下列命题中:
①若x2-3x+2=0,则x=1或x=2
②若-2≤x≤3,则(x+2)(x-3)≤0
③若x=y=0,则x2+y2=0
④若x、y∈N*,x+y是奇数,则x、y中一个是奇数,一个是偶数.
那么( )
①若x2-3x+2=0,则x=1或x=2
②若-2≤x≤3,则(x+2)(x-3)≤0
③若x=y=0,则x2+y2=0
④若x、y∈N*,x+y是奇数,则x、y中一个是奇数,一个是偶数.
那么( )
| A. | ①的逆命题为真 | B. | ②的否命题为假 | C. | ③的逆否命题为假 | D. | ④的逆命题为假 |
11.函数f(x)=x3-3x2在区间[-2,4]上的最大值为( )
| A. | -4 | B. | 0 | C. | 16 | D. | 20 |
5.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x<2}\\{sin(\frac{π}{4}x),2≤x≤10}\end{array}\right.$,若存在实数x1,x2,x3,x4,满足x1<x2<x3<x4,且f(x1)=f(x2)=f(x3)=f(x4),则$\frac{{2{x_3}+{x_4}}}{{{x_1}{x_2}}}$的取值范围是( )
| A. | (4,16) | B. | (0,12) | C. | (9,21) | D. | (14,16) |
12.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$,则目标函数z=x+2y+4的最小值为( )
| A. | 29 | B. | 25 | C. | 11 | D. | 9 |
9.已知条件p:|x+1|>2,条件q:x>a,且¬p是¬q的充分不必要条件,则a的取值范围是( )
| A. | a≤-3 | B. | a≤1 | C. | a≥-1 | D. | a≥1 |
15.有一算法流程图如图所示,该算法解决的是( )
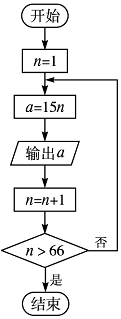

| A. | 输出不大于990且能被15整除的所有正整数 | |
| B. | 输出不大于66且能被15整除的所有正整数 | |
| C. | 输出67 | |
| D. | 输出能被15整除且大于66的正整数 |