��Ŀ����
5����֪����f��x��=$\left\{\begin{array}{l}{|lo{g}_{2}x|��0��x��2}\\{sin��\frac{��}{4}x����2��x��10}\end{array}\right.$��������ʵ��x1��x2��x3��x4������x1��x2��x3��x4����f��x1��=f��x2��=f��x3��=f��x4������$\frac{{2{x_3}+{x_4}}}{{{x_1}{x_2}}}$��ȡֵ��Χ�ǣ�������| A�� | ��4��16�� | B�� | ��0��12�� | C�� | ��9��21�� | D�� | ��14��16�� |
���� ��������f��x����ͼ��ȷ��x1x2=1��x3+x4=12��2��x3��4��8��x4��10���ɴ˿ɵ�$\frac{{2{x_3}+{x_4}}}{{{x_1}{x_2}}}$��ȡֵ��Χ��
��� �⣺������ͼ����ͼ��ʾ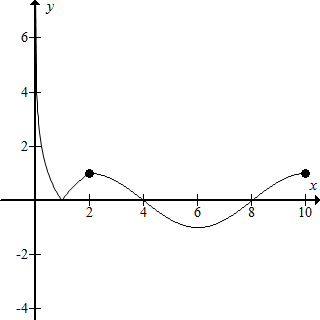
����0��x1��1��x2��2��x3��x4����x3��x4����x=6�Գƣ�
��f��x1��=f��x2����
��-log2x1=log2x2��
��log2x1x2=0��
��x1x2=1��
��f��x3��=f��x4����
��x3+x4=12��2��x3��4��8��x4��10��
��$\frac{{2{x_3}+{x_4}}}{{{x_1}{x_2}}}$=2x3+x4=x3+12��
��$\frac{{2{x_3}+{x_4}}}{{{x_1}{x_2}}}$��ȡֵ��ΧΪ��14��16��
��ѡD��
���� ���⿼��ֶκ�����ͼ����������ֵ���Ӧ�á������뷽�̵��ۺ�Ӧ�õȻ���֪ʶ����������������������ν��������������ת��˼�룬�ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
16���ڡ�ABC�У�D��BC�е㣬AB=8��AC=6����$\overrightarrow{AD}$•$\overrightarrow{BC}$��ֵ�ǣ�������
| A�� | -14 | B�� | -28 | C�� | 14 | D�� | 28 |
17��ִ����ͼ��ʾ�ij����ͼ���������n=5���������SֵΪ��������
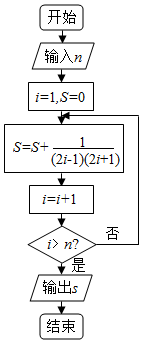

| A�� | $\frac{4}{9}$ | B�� | $\frac{8}{9}$ | C�� | $\frac{5}{11}$ | D�� | $\frac{10}{11}$ |
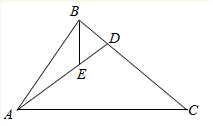 ��ͼ���ڡ�ABC�У���֪��BAC=$\frac{��}{3}$��|$\overrightarrow{AB}$|=2��|$\overrightarrow{AC}$|=3����DΪ��BC��һ�㣬����$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$����E��AD��һ�㣬����$\overrightarrow{AE}$=2$\overrightarrow{ED}$����|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$��
��ͼ���ڡ�ABC�У���֪��BAC=$\frac{��}{3}$��|$\overrightarrow{AB}$|=2��|$\overrightarrow{AC}$|=3����DΪ��BC��һ�㣬����$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$����E��AD��һ�㣬����$\overrightarrow{AE}$=2$\overrightarrow{ED}$����|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$��