题目内容
15．函数f（x）=sinx（x∈[0，π]）的图象与坐标轴围成的图形的面积为m，二项式（mx-3）n的展开式中只有第四项的二项式系数最大，若（mx-3）n=a0+a1x+a2x2+…anxn，则a1+2a2+3a3+…+nan=-12．分析 由题意，m=${∫}_{0}^{π}sinxdx$=$（-cosx）{|}_{0}^{π}$=2，二项式（mx-3）n的展开式中只有第四项的二项式系数最大，则n=6，（2x-3）6=a0+a1x+a2x2+…a6x6，两边同时求导可得12（2x-3）5=a1+2a2 x+3a3 x2+…+6a6x5，再令x=1可得结论．
解答 解：由题意，m=${∫}_{0}^{π}sinxdx$=$（-cosx）{|}_{0}^{π}$=2，
二项式（mx-3）n的展开式中只有第四项的二项式系数最大，则n=6，
（2x-3）6=a0+a1x+a2x2+…a6x6，两边同时求导可得
12（2x-3）5=a1+2a2 x+3a3 x2+…+6a6x5，
再令x=1可得 a1+2a2+3a3+…+6a6=-12，
故答案为-12．
点评 本题主要考查二项式定理的应用，在二项展开式中，通过给变量赋值，求得某些项的系数和，是一种简单
有效的方法，属于中档题．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
6．若函数$f（x）=2sin（ωx+\frac{π}{4}）（ω＞0）$与$g（x）=2cos（2x-\frac{π}{4}）（ω＞0）$的对称轴完全相同，则函数$f（x）=2sin（ωx+\frac{π}{4}）（ω＞0）$在[0，π]上的一个递增区间是（ ）
| A． | $[0，\frac{π}{8}]$ | B． | $[0，\frac{π}{4}]$ | C． | $[\frac{π}{8}，π]$ | D． | $[\frac{π}{4}，π]$ |
3．将一个质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次，记第一次出现的点数为a，第二次出现的点数为b，若已知出现了点数5，则使不等式a-b+3＞0成立的事件发生的概率为（ ）
| A． | $\frac{33}{36}$ | B． | $\frac{3}{4}$ | C． | $\frac{9}{11}$ | D． | $\frac{5}{18}$ |
10．如图，在平面四边形ABCD中，AD=1，CD=2，AC=$\sqrt{7}$．cos∠BAD=-$\frac{\sqrt{7}}{14}$，sin∠CBA=$\frac{\sqrt{21}}{6}$，则BC的长为（ ）
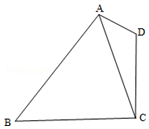
| A． | $\sqrt{7}$ | B． | 2 | C． | 3 | D． | 2$\sqrt{7}$ |
7．函数$y=tan（\frac{π}{4}-x）$的定义域是（ ）
| A． | {x|x≠$\frac{π}{4}$，k∈Z x∈R} | B． | {x|x≠kπ$+\frac{π}{4}$，k∈Z，x∈R} | ||
| C． | {x|x≠$-\frac{π}{4}$，k∈Z x∈R} | D． | {x|x≠kπ$+\frac{3}{4}π$，k∈Z，x∈R} |
如图，已知菱形ABEF所在的平面与△ABC所在的平面相互垂直，AB=4，BC=$\sqrt{6}$，BC⊥BE，∠ABE=$\frac{π}{3}$．