题目内容
函数y=
+
的值域是（ ）
| |cosx| |
| cosx |
| |sinx| |
| sinx |
| A、{0，2} |
| B、{-2，0} |
| C、{-2，0，2} |
| D、{-2，2} |
考点：三角函数值的符号,函数的值域
专题：三角函数的求值
分析：分sinx＞0，cosx＞0；sinx＞0，cosx＜0；sinx＜0，cosx＞0；sinx＜0，cosx＜0四种情况对原函数化简求值得答案．
解答：
解：由题意可知，sinx≠0，cosx≠0．
当sinx＞0，cosx＞0时，y=
+
=2；
当sinx＞0，cosx＜0时，y=
+
=0；
当sinx＜0，cosx＞0时，y=
+
=0；
当sinx＜0，cosx＜0时，y=
+
=-2．
∴函数y=
+
的值域是{-2，0，2}．
故选：C．
当sinx＞0，cosx＞0时，y=
| |cosx| |
| cosx |
| |sinx| |
| sinx |
当sinx＞0，cosx＜0时，y=
| |cosx| |
| cosx |
| |sinx| |
| sinx |
当sinx＜0，cosx＞0时，y=
| |cosx| |
| cosx |
| |sinx| |
| sinx |
当sinx＜0，cosx＜0时，y=
| |cosx| |
| cosx |
| |sinx| |
| sinx |
∴函数y=
| |cosx| |
| cosx |
| |sinx| |
| sinx |
故选：C．
点评：本题考查三角函数的化简与求值，体现了分类讨论的数学思想方法，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知方程|2x-1|=a有两个不等实根，则实数a的取值范围是（ ）
| A、（-∞，0） |
| B、（1，2） |
| C、（0，+∞） |
| D、（0，1） |
正整数按如表的规律排列，则上起第2005行，左起第2006列的数应为（ ）
| A、20052 |
| B、20062 |
| C、2005+2006 |
| D、2005×2006 |
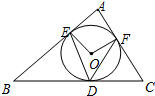如图，⊙O内切于△ABC，切点分别为D，E，F．已知∠B=50°，∠C=60°，连结OE，OF，DE，DF，那么∠EDF等于（ ）| A、40° | B、55° |
| C、65° | D、70° |
设实数a，b，c，d满足ab=c2+d2=1，则（a-c）2+（b-d）2的最小值为（ ）
A、
| ||
B、3+2
| ||
C、
| ||
D、3-2
|
若复数
（a∈R，i为虚数单位）是纯虚数，则实数a的值为（ ）
| a-2i |
| 1+i |
| A、2 | B、-2 | C、1 | D、-1 |
已知数列{an}，满足an+1=
，若a1=
，则a2014=（ ）
| 1 |
| 1-an |
| 1 |
| 2 |
A、
| ||
| B、2 | ||
| C、-1 | ||
| D、1 |
若函数y=|cosx|，（x＞0）与直线y=kx有且仅有两个公共点，其横坐标分别为α、β，且α＜β，则（ ）
A、β=
| ||
B、β=
| ||
C、β=
| ||
D、β=-
|