题目内容
16.已知a,b为实数,函数f(x)=x2+ax+1,且函数y=f(x+1)是偶函数,函数g(x)=-b•f(f(x+1))+(3b-1)•f(x+1)+2在区间(-∞,-2]上的减函数,且在区间(-2,0)上是增函数(1)求函数f(x)的解析式;
(2)求实数b的值;
(3)设h(x)=f(x+1)-2qx+1+2q,问是否存在实数q,使得h(x)在区间[0,2]上有最小值为-2?若存在,求出q的值;若不存在,说明理由.
分析 (1)利用函数y=f(x+1)是偶函数,求函数f(x)的解析式;
(2)利用复合函数的单调性,求实数b的值;
(3)分类讨论,求出函数的最小值,利用h(x)在区间[0,2]上有最小值为-2,得出结论.
解答 解:(1)∵函数y=f(x+1)是偶函数,
∴(x+1)2+a(x+1)+1=(-x+1)2+a(-x+1)+1,
∴4x+2ax=0,
∴a=-2,
∴f(x)=(x-1)2;
(2)g(x)=-b•f(f(x+1))+(3b-1)•f(x+1)+2=-bx4+(5b-1)x2+2-b,
令t=x2,u(t)=-bt2+(5b-1)t-(b-2),
在区间(-∞,-2]上,t=x2是减函数,且t∈[4,+∞),由g(x)是减函数,可知u(t)为增函数;
在区间(-2,0)上,t=x2是减函数,且t∈(0,4),由g(x)是增函数,可知u(t)为减函数,
∴由u(t)在(0,4)上是减函数,(4,+∞)上是增函数,
可得二次函数开口向上,b<0,且-$\frac{5b-1}{-2b}$=4,∴b=-$\frac{1}{3}$;
(3)h(x)=f(x+1)-2qx+1+2q=x2=2qx+2q,x∈[0,2].
q<0,ymin=h(0)=1+2q=-2,q=-$\frac{3}{2}$;
0≤q≤2,ymin=h(q)=-q2+2q+1=-2,∴q=3或-1,舍去;
q>2,ymin=h(2)=-2q+5=-2,q=$\frac{7}{2}$,
综上所述,q=-$\frac{3}{2}$或$\frac{7}{2}$.
点评 本题考查函数的性质,考查函数解析式的求解,考查学生的最值,正确分类讨论是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.记不等式组$\left\{\begin{array}{l}4x+3y≥10\\ x≤5\\ y≤4\end{array}\right.$表示的平面区域为D,过区域D中任意一点P作圆x2+y2=1的两条切线,切点分别为A,B,则当∠APB的最大时,cos∠APB为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
1.设$lnx=\frac{{{{ln}^2}sinα}}{lnb},lny=\frac{{{{ln}^2}cosα}}{lnb},lnz=\frac{{{{ln}^2}sinαcosα}}{lnb}$,若$α∈({\frac{π}{4},\frac{π}{2}}),b∈({0,1})$,则x,y,z的大小关系为( )
| A. | x>y>z | B. | y>x>z | C. | z>x>y | D. | x>z>y |
8.在$(2{x}^{2}-\frac{1}{\sqrt{x}})^{6}$的展开式中,含x7的项的系数是( )
| A. | 60 | B. | 160 | C. | 180 | D. | 240 |
5.直线x+ay+6=0与直线(a-2)x+3y+2a=0平行,则a的值为( )
| A. | 3 或-1 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
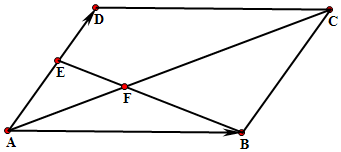 如图,平行四边形ABCD中,点E在线段AD上,BE与AC交于点F,设$\overrightarrow{AB}=a,\overrightarrow{AD}=b$.
如图,平行四边形ABCD中,点E在线段AD上,BE与AC交于点F,设$\overrightarrow{AB}=a,\overrightarrow{AD}=b$.