题目内容
6.△ABC的内角A,B,C的对边分别为a,b,c,若$cosA=-\frac{3}{5}$,$sinC=\frac{1}{2}$,c=1,则△ABC的面积为$\frac{8\sqrt{3}-6}{25}$.分析 利用正弦定理、和差公式、三角形面积计算公式即可得出.
解答 解:∵2R=$\frac{c}{sinC}$=2,则$a=2RsinA=2×\frac{4}{5}=\frac{8}{5}$,
又sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{4}{5}×\frac{{\sqrt{3}}}{2}+({-\frac{3}{5}})×\frac{1}{2}=\frac{{4\sqrt{3}-3}}{10}$,
∴$S=\frac{1}{2}acsinB=\frac{1}{2}×\frac{8}{5}×1×\frac{{4\sqrt{3}-3}}{10}=\frac{{8\sqrt{3}-6}}{25}$.
故答案为:$\frac{8\sqrt{3}-6}{25}$.
点评 本题考查了正弦定理、和差公式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.△ABC的顶点A(5,0),B(-5,0),△ABC的周长为22,则顶点C的轨迹方程是( )
| A. | $\frac{x^2}{36}+\frac{y^2}{11}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{11}=1$ | ||
| C. | $\frac{x^2}{36}+\frac{y^2}{11}=1({y≠0})$ | D. | $\frac{x^2}{9}+\frac{y^2}{16}=1({y≠0})$ |
1.下列说法正确的是( )
| A. | 若p∧q为假命题,则p、q均为假命题 | |
| B. | 命题“若x2=1,则x=1”为真命题 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“存在一个实数x,使不等式x2-3x+6<0成立”为真命题 |
11.若点P是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的渐近线上任意一点,下列正确的是( )
| A. | 存在过点P的直线与双曲线相切 | |
| B. | 不存在过点P的直线与双曲线相切 | |
| C. | 至少存在一条过点P的直线与该双曲线没有交点 | |
| D. | 存在唯一过点P的直线与该双曲线没有交点 |
18.以原点为顶点,x轴为对称轴的抛物线的焦点在直线2x-4y-11=0上,则此抛物线的方程是( )
| A. | y2=11x | B. | y2=-11x | C. | y2=22x | D. | y2=-22x |
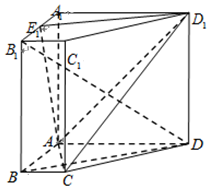 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,AB=$\sqrt{3}$,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,AB=$\sqrt{3}$,E1为A1B1中点.