题目内容
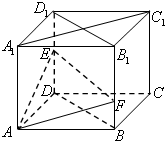
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2BF.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2BF.(1)求证:EF⊥A1C1;
(2)在棱C1C上确定一点G,使A、E、G、F四点共面,并求此时C1G的长;
(3)求几何体ABFED的体积.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(1)连结B1D1,BD,由已知条件推导出A1C1⊥DD1,从而得到A1C1⊥平面BB1D1D.由此能证明EF⊥A1C1.
(2)以点D为坐标原点,以DA,DC,DD1所在的直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出当C1G=
a时,A,E,G,F四点共面.
(3)以BFED为底,A到平面的距离为高,即可求出几何体ABFED的体积.
(2)以点D为坐标原点,以DA,DC,DD1所在的直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出当C1G=
| 1 |
| 6 |
(3)以BFED为底,A到平面的距离为高,即可求出几何体ABFED的体积.
解答:
(1)证明:连结B1D1,BD,∵四边形A1B1C1D1是正方形,∴B1D1⊥A1C1.
 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,
∵DD1⊥平面A1B1C1D1,A1C1?平面A1B1C1D1,∴A1C1⊥DD1.
∵B1D1∩DD1=D1,B1D1,DD1?平面BB1D1D,∴A1C1⊥平面BB1D1D.
∵EF?平面BB1D1D,∴EF⊥A1C1.
(2)解:以点D为坐标原点,以DA,DC,DD1所在的直线分别为x轴,y轴,z轴,建立如图的空间直角坐标系,
 则A(a,0,0),A1(a,0,a),C1(0,a,a),E(0,0,
则A(a,0,0),A1(a,0,a),C1(0,a,a),E(0,0,
a),F(a,a,
a),
∴
=(-a,a,0),
=(-a,a,0),
=(a,a,-
a).
设G(0,a,h),
∵平面ADD1A1∥平面BCC1B1,平面ADD1A1∩平面AEGF=AE,
平面BCC1B1∩平面AEGF=FG,
∴存在实数λ,使得
=λ
.
∵
=(-a,0,
a),
=(-a,0,h-
a),
∴λ=1,h=
a
∴C1G=
a.
∴当C1G=
a时,A,E,G,F四点共面.
(3)解:几何体ABFED的体积为
•
•(
+
)•
a•
a=
a3.
 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,∵DD1⊥平面A1B1C1D1,A1C1?平面A1B1C1D1,∴A1C1⊥DD1.
∵B1D1∩DD1=D1,B1D1,DD1?平面BB1D1D,∴A1C1⊥平面BB1D1D.
∵EF?平面BB1D1D,∴EF⊥A1C1.
(2)解:以点D为坐标原点,以DA,DC,DD1所在的直线分别为x轴,y轴,z轴,建立如图的空间直角坐标系,
 则A(a,0,0),A1(a,0,a),C1(0,a,a),E(0,0,
则A(a,0,0),A1(a,0,a),C1(0,a,a),E(0,0,| 1 |
| 2 |
| 1 |
| 3 |
∴
| A1C1 |
| EF |
| EF |
| 1 |
| 6 |
设G(0,a,h),
∵平面ADD1A1∥平面BCC1B1,平面ADD1A1∩平面AEGF=AE,
平面BCC1B1∩平面AEGF=FG,
∴存在实数λ,使得
| FG |
| AE |
∵
| AE |
| 1 |
| 2 |
| FG |
| 1 |
| 3 |
∴λ=1,h=
| 5 |
| 6 |
∴C1G=
| 1 |
| 6 |
∴当C1G=
| 1 |
| 6 |
(3)解:几何体ABFED的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| a |
| 3 |
| a |
| 2 |
| ||
| 2 |
| 2 |
| 5 |
| 36 |
点评:本小题主要考查空间线面关系、四点共面、二面角的平面角、空间向量及坐标运算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
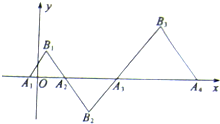 如图,在直角坐标平面xOy中,△AjBjAj+1(其中j=1,2,n,…)为正三角形,且满足
如图,在直角坐标平面xOy中,△AjBjAj+1(其中j=1,2,n,…)为正三角形,且满足