题目内容
已知m=cos(-4),n=sin(-4),则( )
| A、m>n | B、m<n |
| C、m=n | D、m与n的大小不确定 |
考点:三角函数线
专题:三角函数的求值
分析:根据m=-cos(4-π),n=-sin(4-π),4-π∈(
,
),可得sin(4-π)>cos(4-π),从而得到m、n的大小关系.
| π |
| 4 |
| π |
| 2 |
解答:
解:m=cos(-4)=cos4=-cos(4-π),n=sin(-4)=-sin4=-sin(4-π),
∵4-π∈(
,
),∴sin(4-π)>cos(4-π),∴-sin(4-π)<-cos(4-π),
∴m>n,
故选:A.
∵4-π∈(
| π |
| 4 |
| π |
| 2 |
∴m>n,
故选:A.
点评:本题主要考查诱导公式、正弦函数的、余弦函数在(
,
)上的值,体现了转化的数学思想,属于基础题.
| π |
| 4 |
| π |
| 2 |

练习册系列答案
相关题目
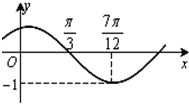 函数f(x)=sin(ωx+φ)(其中|φ|<
函数f(x)=sin(ωx+φ)(其中|φ|<| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
 如图,已知△ABC中,D为BC的中点,E,F为BC的三等分点,若
如图,已知△ABC中,D为BC的中点,E,F为BC的三等分点,若