题目内容
已知数据:x,y,10,11,9,这组数据的平均值10,方差为2,则|x-y|= .
考点:众数、中位数、平均数,极差、方差与标准差
专题:概率与统计
分析:利用平均数、方差的概念列出关于x、y的方程组,解这个方程组需要用一些技巧,因为不要直接求出x、y,只要求出|x-y|即可,故可设x=10+t,y=10-t,求解即可.
解答:
解:由平均值10得,x+y+10+11+9=50,则x+y=20,①
由方差为2得,2=
[(x-10)2+(y-10)2+0+1+1],
即(x-10)2+(y-10)2=8,②
设x=10+t,y=10-t,代入②2t2=8,解得t=±2,
∴|x-y|=2|t|=4,
故答案为:4.
由方差为2得,2=
| 1 |
| 5 |
即(x-10)2+(y-10)2=8,②
设x=10+t,y=10-t,代入②2t2=8,解得t=±2,
∴|x-y|=2|t|=4,
故答案为:4.
点评:本题考查统计的基本知识,样本平均数与样本方差的概念以及求解方程组的方法,比较简单.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
若关于实数x的不等式x3-3x2-9x≥m对任意x∈[-2,2]恒成立,则m的取值范围是( )
| A、(-∞,5] |
| B、(-∞,-22] |
| C、(-∞,-2] |
| D、[-14,5] |
某几何体的三视图(单位:cm)如图所示,则该几何体的体积为:( )
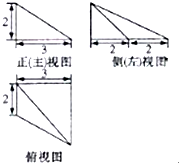

| A、2cm2 | ||
B、
| ||
C、
| ||
| D、6cm2 |
椭圆的焦点坐标为(4,0),(-4,0),椭圆上一点到两焦点的距离之和为10,则椭圆的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知圆M:(x+2)2+y2=4,过点P(-1,0)作圆M的互相垂直的两条弦AB,CD,则这两条弦长之和的最大值为( )
A、2
| ||
| B、8 | ||
C、4+2
| ||
D、4
|
设α为锐角,且cos(α+
)=
,则sin(α-
)的值为( )
| π |
| 3 |
| 4 |
| 5 |
| π |
| 6 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
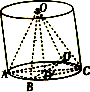 在一个圆柱中挖去一个内接正四棱锥O-ABCD(顶点是上面底面积圆的圆心O,底面是下底面的内接正方形),得到如图所示的几何体,已知圆柱底面直径为4
在一个圆柱中挖去一个内接正四棱锥O-ABCD(顶点是上面底面积圆的圆心O,底面是下底面的内接正方形),得到如图所示的几何体,已知圆柱底面直径为4