题目内容
若极坐标系中曲线方程为ρcos2
=1,以极点为原点,极轴为X轴正半轴建立直角坐标系,则该曲线的直角坐标方程为 .
| θ |
| 2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:本题可以利用极坐标与直角坐标的关系,求出曲线的直角坐标方程.
解答:
解:∵在极坐标系中曲线方程为ρcos2
=1,
∴
ρ(1+cosθ)=1,
∴ρ+ρcosθ=2.
∵
,
∴
+x=2,
∴该曲线的直角坐标方程为y2=-4(x-1).
| θ |
| 2 |
∴
| 1 |
| 2 |
∴ρ+ρcosθ=2.
∵
|
∴
| x2+y2 |
∴该曲线的直角坐标方程为y2=-4(x-1).
点评:本题考查的极坐标与直角坐标的关系,三角函数的半角公式,本题难度不大,属于基础题.

练习册系列答案
相关题目
(文科)已知-3<a<-2,3<b<4,则
的取值范围为( )
| a2 |
| b |
| A、(1,3) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
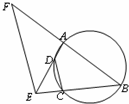 如图,A、B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.
如图,A、B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.