题目内容
设f(x)的定义域为D,若f(x)满足下面两个条件则称f(x)为闭函数:①f(x)是D上的单调函数;②存在[a,b]⊆D,使f(x)在[a,b]上的值域为[a,b].现已知f(x)=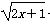 +k为闭函数,则k的取值范围是( )
+k为闭函数,则k的取值范围是( )
A.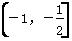 B.(-∞,1)
B.(-∞,1)
C.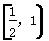 D.(-1,+∞)
D.(-1,+∞)
A
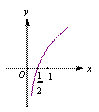
[解析] 如图,函数的定义域为x∈-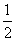 ,+∞,显然在定义域上函数f(x)单调递增,依题可知,在x∈
,+∞,显然在定义域上函数f(x)单调递增,依题可知,在x∈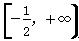 上,方程x-k=
上,方程x-k=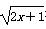 有两个不同的解,结合图象易得实数k的取值范围为-1<k≤-
有两个不同的解,结合图象易得实数k的取值范围为-1<k≤-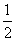 .
.


练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
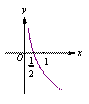
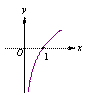
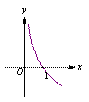
函数f(x)=log2(2x)的图象大致是 ( )
|
|
|
|
|
| A. | B. | C. | D. |
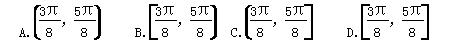
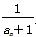 ,记Sn为数列{an}的前n项和,则S2 014=________.
,记Sn为数列{an}的前n项和,则S2 014=________.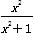 ,则f(1)+f(2)+…+f(2 013)+f(2 014)+
,则f(1)+f(2)+…+f(2 013)+f(2 014)+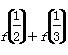 +…+
+…+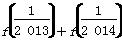 =( )
=( )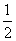 B.2 011
B.2 011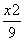 -
-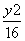 =1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为( )
=1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为( )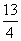 或
或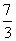 B.
B.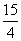 或
或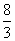 C.
C.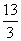 D.
D.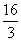
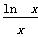 ,其中a∈R.
,其中a∈R.