题目内容
已知函数f(x)=ax+1+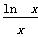 ,其中a∈R.
,其中a∈R.
(1)若f(x)在定义域上单调递增,求实数a的取值范围;
(2)若函数g(x)=xf(x)有唯一零点,试求实数a的取值范围.
B
B
[解析] 由an<bn,得-(-1)n·a<2+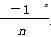 ,
,
要使其对任意n∈N*恒成立,则当n=2k-1(k∈N*)时,a<2-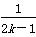 恒成立,又
恒成立,又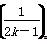 max=1,所以a<2-1=1;当n=2k(k∈N*)时,-a<2+
max=1,所以a<2-1=1;当n=2k(k∈N*)时,-a<2+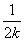 恒成立,又
恒成立,又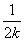 ∈
∈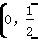 ,所以-a≤2,得a≥-2.综上所述,-2≤a<1.
,所以-a≤2,得a≥-2.综上所述,-2≤a<1.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
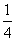 (b2+c2-a2),则角B等于( )
(b2+c2-a2),则角B等于( )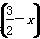 =f(x),f(-2)=5,数列{an}满足a1=-1,且
=f(x),f(-2)=5,数列{an}满足a1=-1,且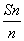 =2×
=2×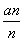 +1(其中Sn为{an}的前n项和),则f(a6)+f(a7)=________.
+1(其中Sn为{an}的前n项和),则f(a6)+f(a7)=________.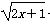 +k为闭函数,则k的取值范围是( )
+k为闭函数,则k的取值范围是( )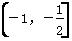 B.(-∞,1)
B.(-∞,1)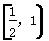 D.(-1,+∞)
D.(-1,+∞)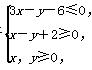
 B.
B.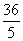 C.
C.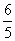 D.
D.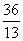
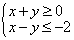 ,则x+2y的最小值为 ( )
,则x+2y的最小值为 ( )