题目内容

20．已知点（a，$\frac{1}{3}$）在幂函数f（x）=（a2-6a+10）xb的图象上，则函数f（x）是（　　）
A．奇函数B．偶函数
C．定义域内的减函数D．定义域内的增函数

分析 根据幂函数的定义与性质，列出方程求出a与b的值，求出f（x）的解析式，即可得出结论．

解答 解：幂函数f（x）=（a2-6a+10）•xb的图象经过点（a，$\frac{1}{3}$），
∴a2-6a+10=1且ab=$\frac{1}{3}$，
解得a=3，b=-1；
∴f（x）=x-1在定义域（-∞，0）∪（0，+∞）的奇函数．
故选：A．

点评 本题考查了幂函数的定义与性质的应用问题，是基础题目．

练习册系列答案
相关题目
10．阅读如图的程序框图，当该程序运行后输出的x值是（　　）
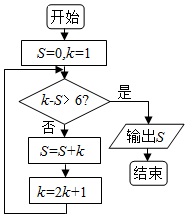
A．57B．63C．110D．120
11．已知函数y=f（1-x）的图象如图，则y=|f（x+2）|的图象是（　　）
A．B．C．D．
8．已知集合A={1，2，4}，B={m，4，7}，若A∩B={1，4}，则A∪B={1，2，4，7}．
15．在1和16之间插入3个数，使它们与这两个数依次构成等比数列，则这3个数的积（　　）
A．128B．±128C．64D．±64
5．已知集合M={x|2x≥1，x∈R}，集合N={x||x-2|≥3，x∈R}，则M∩N=（　　）
A．（-∞，-1]B．[-1，0]C．[5，+∞）D．∅
12．2015年4月22日，亚非领导人会议在印尼雅加达举行，某五国领导人A、B、C、D、E除B与E、D与E不单独会晤外，其他领导人两两之间都要单独会晤．现安排他们在两天的上午、下午单独会晤（每人每个半天最多只进行一次会晤），那么安排他们单独会晤的不同方法共有48种．
9．下列函数中，既是偶函数，又在（0，+∞）单调递增的函数是（　　）
A．y=-x2B．y=2-|x|C．y=|$\frac{1}{x}$|D．y=lg|x|
10．若数列{an}满足a11=$\frac{1}{52}$，$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=5（n∈N*），则a1=$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网