题目内容
已知函数f(x)=
sin2x+
cos2x,x∈R.
(1)求f(x)的最小正周期和递减区间;
(2)若f(
-
)=
,α是第二象限的角,求sin2α.
| 2 |
| 2 |
(1)求f(x)的最小正周期和递减区间;
(2)若f(
| α |
| 2 |
| π |
| 8 |
| ||
| 2 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质
分析:(1)把给出的函数化积为y=Asin(ωx+φ)的形式,则周期可求,由正弦型复合函数的单调性求解减区间;
(2)把f(
-
)=
代入(1)中的函数解析式,结合α的范围求解α的正余弦值,由倍角公式得答案.
(2)把f(
| α |
| 2 |
| π |
| 8 |
| ||
| 2 |
解答:
解(1)∵f(x)=
sin2x+
cos2x
=2(
sin2x+
cos2x)
=2(cos
sin2x+sin
cos2x)
=2sin(2x+
),
∴f(x)的最小正周期为T=
=π,
由2kπ+
≤2x+
≤2kπ+
,得
kπ+
≤x≤kπ+
(k∈Z),
∴函数的递减区间是[kπ+
,kπ+
]( k∈Z);
(2)由(1)知,f(x)=2sin(2x+
),
∴f(
-
)=2sinα=
,即sinα=
,
又α是第二象限的角,
∴cosα=-
=-
=-
,
∴sin2α=2sinαcosα=2×
×(-
)=-
.
| 2 |
| 2 |
=2(
| ||
| 2 |
| ||
| 2 |
=2(cos
| π |
| 4 |
| π |
| 4 |
=2sin(2x+
| π |
| 4 |
∴f(x)的最小正周期为T=
| 2π |
| 2 |
由2kπ+
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
kπ+
| π |
| 8 |
| 5π |
| 8 |
∴函数的递减区间是[kπ+
| π |
| 8 |
| 5π |
| 8 |
(2)由(1)知,f(x)=2sin(2x+
| π |
| 4 |
∴f(
| α |
| 2 |
| π |
| 8 |
| ||
| 2 |
| ||
| 4 |
又α是第二象限的角,
∴cosα=-
| 1-sin2α |
1-(
|
| ||
| 4 |
∴sin2α=2sinαcosα=2×
| ||
| 4 |
| ||
| 4 |
| ||
| 8 |
点评:本题考查了三角函数中的恒等变换的应用,训练了与三角函数有关的复合函数的单调性的求法,考查了二倍角的正弦公式,是中档题.

练习册系列答案
相关题目
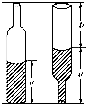 如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为( )
如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为( )A、1+
| ||
B、1+
| ||
C、1+
| ||
D、1+
|
随机试验,同时掷三颗骰子,记录三颗骰子的点数之和,试验的基本事件总数是( )
| A、15 | B、16 | C、17 | D、18 |