题目内容
16.解关于x的不等式:$\frac{ax}{x-1}≤1$.分析 分当a>1、当a=1、当0<a<1,a=0,a<0情况,分别求出不等式的解集.
解答 解::$\frac{ax}{x-1}≤1$可得$\frac{ax}{x-1}$-1≤0,即$\frac{(a-1)x+1}{x-1}$≤0,
等价于[(a-1)x+1](x-1)≤0,且x≠1,
当a>1时,解得$\frac{1}{1-a}$≤x<1,
当a=1时,解得x<1,
当a<1时,不等式化简为(x-$\frac{1}{1-a}$)(x-1)≥0,且x≠1
①当0<a<1时,解得x<1或x≥$\frac{1}{1-a}$,
②当a=0时,解得x≠1,
③当a<0时,解得x≤$\frac{1}{1-a}$或x>1,
综上所述,当a>1时,不等式的解集为[$\frac{1}{1-a}$,1),
当a=1时,不等式的解集为(-∞,1),
当0<a<1时,不等式的解集为(-∞,1)∪[$\frac{1}{1-a}$,+∞),
当a=0时,不等式的解集为(-∞,0)∪(0,+∞),
当a<0时,不等式的解集为(-∞,$\frac{1}{1-a}$]∪(1,+∞).
点评 本题主要考查一元二次不等式、分式不等式的解法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.为迎接春节,某工厂大批生产小孩玩具--拼图,工厂为了规定工时定额,需要确定加工拼图所花费的时间,为此进行了5次试验,测得的数据如下:
(1)画出散点图,并判断y与x是否具有相关关系;
(2)求回归方程;
(3)根据求出的回归方程,预测加工2 00个拼图需用多少分钟.
| 拼图数x/个 | 10 | 20 | 30 | 40 | 50 |
| 加工时间y/分钟 | 62 | 68 | 75 | 81 | 89 |
(2)求回归方程;
(3)根据求出的回归方程,预测加工2 00个拼图需用多少分钟.
1.已知偶函数f(x)的定义域为R,若f(x-1)为奇函数,且f(2)=3,则f(5)+f(6)的值为( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |

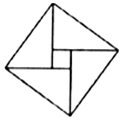 第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.
第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.