题目内容

9．已知a，b∈（0，1）记M=a•b，N=a+b-1则M与N的大小关系是（　　）
A．M＜NB．M=NC．M＞ND．不确定

分析 作差利用不等式的性质即可得出．

解答 解：a，b∈（0，1），记M=a•b，N=a+b-1，
∴M-N=a•b-a-b+1=（1-a）（1-b）＞0，
∴M＞N．
故选：C．

点评 本题考查了作差法、不等式的性质，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
19．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{2}=1$（a＞0）的离心率为2，则a的值为$\frac{{\sqrt{6}}}{3}$．
20．在（$\root{3}{2}$x2$-\frac{1}{\root{3}{2}x}$）4的展开式中，系数为有理数的项为（　　）
A．第二项B．第三项C．第四项D．第五项
17．设a≠0，函数f（x）=$\left\{\begin{array}{l}{4lo{g}_{2}（-x），x＜0}\\{|{x}^{2}+ax|，x≥0}\end{array}\right.$，若f[f（-$\sqrt{2}$）]=4，则f（a）等于（　　）
A．8B．4C．2D．1
4．己知实数x，y满足不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{2x+y-3≤0}\\{0≤y≤a}\end{array}\right.$，若z=x-2y的最小值为-3，则a的值为（　　）
A．1B．$\frac{3}{2}$C．2D．$\frac{7}{3}$
14．在公差不为零的等差数列{an}中，$2{a_3}+2{a_{11}}=a_7^2$，数列{bn}是各项为正的等比数列，且b7=a7则b6b8的值为（　　）
A．2B．1C．4D．16
1．已知f（x）=loga（x-1）+1（a＞0且a≠1）恒过定点M，且点M在直线$\frac{x}{m}+\frac{y}{n}=1$（m＞0，n＞0）上，则m+n的最小值为（　　）
A．$3+2\sqrt{2}$B．8C．$4\sqrt{2}$D．4
18．若y=f（x）是定义域在R上的函数，则y=f（x）为奇函数的一个充要条件为（　　）
A．f（0）=0B．对?x∈R，f（x）=0都成立
C．?x0∈R，使得f（x0）+f（-x0）=0D．对?x∈R，f（x）+f（-x）=0都成立
7．如图给出了计算S=$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{60}$的值的程序框图，其中 ①②分别是（　　）
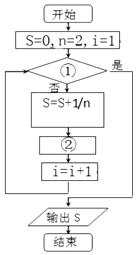
A．i＜30，n=n+2B．i＞30，n=n+2C．i＜30，n=n+1D．i＞30，n=n+1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网