题目内容
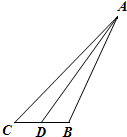 如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cos2α=-
如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cos2α=-| 1 |
| 25 |
(1)求cosα;
(2)求BC边上高的值.
考点:解三角形的实际应用
专题:综合题,解三角形
分析:(1)由二倍角公式cos2α=2cos2α-1,可求cosα
(2)作BC 边上的高为AH,在直角△ADH中,由(1)可得cosα=
=
,设出AD,则可表示DH,AH,结合△AHC为等腰直角三角形,可得CD+DH=AH,代入可求
(2)作BC 边上的高为AH,在直角△ADH中,由(1)可得cosα=
| DH |
| AD |
2
| ||
| 5 |
解答:
解:(1)∵cos2α=2cos2α-1=-
,
∴cos2α=
,
∵α是锐角,
∴cosα=
.-----------(5分)
(2) 如图,作BC 边上的高为AH
如图,作BC 边上的高为AH
在直角△△ADH中,由(1)可得cosα=
=
,
则不妨设AD=5m,则DH=2
m,AH=
m-----------------(8分)
注意到C=45°,则△AHC为等腰直角三角形,所以CD+DH=AH,
则1+2
m=
m-----------------(10分)
所以m=
+2
,即AH=13+2
-----------------(12分)
| 1 |
| 25 |
∴cos2α=
| 12 |
| 25 |
∵α是锐角,
∴cosα=
2
| ||
| 5 |
(2)
 如图,作BC 边上的高为AH
如图,作BC 边上的高为AH 在直角△△ADH中,由(1)可得cosα=
| DH |
| AD |
2
| ||
| 5 |
则不妨设AD=5m,则DH=2
| 3 |
| 13 |
注意到C=45°,则△AHC为等腰直角三角形,所以CD+DH=AH,
则1+2
| 3 |
| 13 |
所以m=
| 13 |
| 3 |
| 39 |
点评:本题主要考查了同角平方关系、和差角公式及正弦定理在求解三角形中的应用,解题的关键是熟练应用基本公式.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
∫
sin2
dx=( )
0 |
| x |
| 2 |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|