题目内容
二项式(1-x2)5的展开式中x6的系数为 .
考点:二项式系数的性质
专题:二项式定理
分析:根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x的指数为6求得r,再代入系数求出结果.
解答:
解:根据所给的二项式(1-x2)5,写出展开式的通项,
Tr+1=(-1)r
x2r;
要求x6的项的系数
∴2r=6,
∴r=3,
∴x6的项的系数是-C53=-10
故答案为:10.
Tr+1=(-1)r
| C | r 5 |
要求x6的项的系数
∴2r=6,
∴r=3,
∴x6的项的系数是-C53=-10
故答案为:10.
点评:本题考查二项式定理的应用,本题解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.

练习册系列答案
相关题目
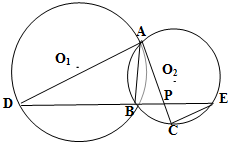 如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为
如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为 如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,PC=2,PB=4,则CD=
如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,PC=2,PB=4,则CD=