题目内容

17．抛掷两枚骰子，当至少有一枚5点或6点出现时，就说试验成功，则在30次独立重复试验中成功的次数X的数学期望是（　　）
A．$\frac{40}{3}$B．$\frac{50}{3}$C．10D．20

分析 由题意知试验中的事件是相互独立的，事件发生的概率是相同的，得到成功次数ξ服从二项分布，根据二项分布的期望公式得到结果．

解答 解：∵成功次数ξ服从二项分布，
每次试验成功的概率为1-$\frac{2}{3}$×$\frac{2}{3}$=$\frac{5}{9}$，
∴在30次试验中，成功次数ξ的期望为 $\frac{5}{9}$×30=$\frac{50}{3}$．
故选：B．

点评 二项分布要满足的条件：每次试验中，事件发生的概率是相同的，各次试验中的事件是相互独立的，每次试验只要两种结果，要么发生要么不发生，随机变量是这n次独立重复试验中事件发生的次数．

练习册系列答案
相关题目
4．已知函数f（x）=x（x-m）2在x=2处取得极小值，则常数m的值为（　　）
A．2B．6C．2或6D．以上答案都不对
5．已知函数f（x）=ax2-lnx（a∈R）
（1）当a=1时，求函数y=f（x）的单调区间；
（2）若?x∈（0，1]，|f（x）|≥1恒成立，求a的取值范围；
（3）若a=$\frac{e}{2}$，证明：ex-1f（x）≥x．
5．三位同学乘同一列火车，火车有10节车厢，则至少有2位同学上了同一车厢的概率为$\frac{7}{25}$．
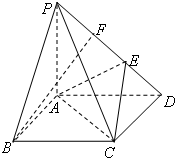12．四棱锥P-ABCD的底面是边长为1的正方形，PA⊥CD，PA=1，PD=$\sqrt{2}$，E，F为PD上两点，且PF=ED=$\frac{1}{3}$PD．
（1）求证：BF∥面ACE；
（2）求异面直线PC与AE所成角的余弦值；
（3）求二面角P-AC-E的余弦值．
2．数列{an}满足$\frac{{a}_{1}}{1}$+$\frac{{a}_{2}}{3}$+$\frac{{a}_{3}}{5}$+…+$\frac{{a}_{n}}{2n-1}$=3n+1，则数列{an}的通项公式为an=（2n-1）•2•3n．
9．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的一个焦点$F（\sqrt{3}，0）$，长轴顶点到点A（0，-2）的距离为2$\sqrt{2}$，O为坐标原点．
（1）求椭圆C的方程；
（2）设过A点的动直线l与椭圆C相交于M，N两点，当△OMN的面积最大时，求l的方程．
6．已知函数f（x）=2x3-3x2-12x
（1）求f（x）=2x3-3x2-12x的极值；
（2）设函数g（x）=2x3-3x2-12x+a的图象与x轴有两个交点，求a的值．
7．设函数y=f（x）在区间D上的导函数为f′（x），f′（x）在区间D上的导函数为g（x）．若在区间D上，g（x）＜0恒成立，则称函数f（x）在区间D上为“凸函数”．已知实数m是常数，f（x）=$\frac{x^4}{12}-\frac{{m{x^3}}}{6}-\frac{{3{x^2}}}{2}$，若对满足|m|≤2的任何一个实数m，函数f（x）在区间（a，b）上都为“凸函数”，则b-a的最大值为（　　）
A．3B．2C．1D．-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网