题目内容
11.已知三棱锥S-ABC所有顶点都在球O的球面上,且SC⊥平面ABC,若AC=AB=1,SC=2,∠BAC=120°,则球D的表面积为8π.分析 求出BC,可得△ABC外接圆的半径,从而可求该三棱锥的外接球的半径,即可求出三棱锥的外接球表面积.
解答 解:∵AB=1,AC=1,∠BAC=120°,
∴BC=$\sqrt{1+1-2×1×1×(-\frac{1}{2})}$=$\sqrt{3}$,
∴三角形ABC的外接圆直径2r=$\frac{\sqrt{3}}{sin120°}$=2,
∴r=1,
∵SC⊥面ABC,SC=2,三角形OSC为等腰三角形,
∴该三棱锥的外接球的半径R=$\sqrt{2}$,
∴该三棱锥的外接球的表面积为S=4πR2=4π×($\sqrt{2}$)2=8π.
故答案为:8π.
点评 本题考查三棱锥的外接球表面积,考查直线和平面的位置关系,确定三棱锥的外接球的半径是关键.

练习册系列答案
相关题目
10.化简cos2($\frac{x}{2}$-$\frac{7π}{8}$)-cos2($\frac{x}{2}$+$\frac{7π}{8}$)的结果为( )
| A. | $\frac{\sqrt{2}}{2}$cosx | B. | -$\frac{\sqrt{2}}{2}$cosx | C. | -$\frac{\sqrt{2}}{2}$sinx | D. | $\frac{\sqrt{2}}{2}$sinx |
6.若过原点的直线l的倾斜角是直线:y=x的倾斜角的两倍,则l的方程是( )
| A. | y=2x | B. | y=0 | C. | x=0 | D. | y=$\frac{1}{2}$x |
20.已知函数f(x)=x2+x-2,x∈[-1,6],若在其定义域内任取一数x0使得f(x0)≤0概率是( )
| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
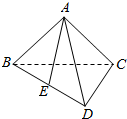 如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.
如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.